Dette verktøyet beregner verdien av et hvilket som helst tall hevet til en gitt eksponent. Skriv inn en base og en eksponent, så vil kalkulatoren vise resultatet sammen med beregningsstegene. Ideelt for studenter, ingeniører og alle som arbeider med potenser, støtter dette verktøyet både heltall og desimaler. Dette verktøyet er spesielt nyttig for norske studenter og fagfolk som trenger å utføre eksponentielle beregninger i sitt daglige arbeid.
Eksponentiell Kalkulator
xn = a
Grunnnummer (x)
Eksponent (n)
Resultat (a)
Slik bruker du denne kalkulatoren
- Angi base (x): Skriv inn tallet du ønsker å heve til en eksponent.
- Angi eksponent (n): Skriv inn potensen som basen skal heves til.
- Se resultat (a): Resultatet beregnes automatisk og vises.
- Sjekk steg: En oppdeling av beregningen vises under resultatet.
- Kopier resultat: Klikk «Kopier resultat» for å lagre utdataene til utklippstavlen.
- Nullstill: Klikk «Nullstill alt» for å tilbakestille alle felt og starte en ny beregning.
Verditabell
| x | x² | x³ | x⁴ | x⁵ |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 4 | 8 | 16 | 32 |
| 3 | 9 | 27 | 81 | 243 |
| 4 | 16 | 64 | 256 | 1024 |
| 5 | 25 | 125 | 625 | 3125 |
| 6 | 36 | 216 | 1296 | 7776 |
| 7 | 49 | 343 | 2401 | 16807 |
| 8 | 64 | 512 | 4096 | 32768 |
| 9 | 81 | 729 | 6561 | 59049 |
| 10 | 100 | 1000 | 10000 | 100000 |
Forstå eksponentiering
Eksponentiering er en matematisk operasjon som involverer å heve et basisnummer (x) til potensen av en eksponent (n). Det skrives som xⁿ og betyr å multiplisere basen med seg selv n ganger. For eksempel, 3² = 3 × 3 = 9.
Grunnleggende konsept
I uttrykket xⁿ:
- x er basen — tallet som blir multiplisert.
- n er eksponenten — den forteller hvor mange ganger basen multipliseres med seg selv.
- a er resultatet — den endelige verdien av operasjonen.
Hva er en negativ eksponent?
En negativ eksponent betyr den omvendte av basen hevet til den motsatte positive potensen. For eksempel:
- 2⁻¹ = 1 / 2¹ = 1/2
- 3⁻² = 1 / (3²) = 1/9
Generelt er x⁻ⁿ = 1 / xⁿ for enhver ikke-null base x.
Hva er en desimal- eller brøkeksponent?
Desimal- eller brøkeksponenter representerer røtter. For eksempel:
- x0.5 = √x (kvadratroten av x)
- x0.25 = ⁴√x (fjerde roten av x)
- x1.5 = x × √x
Generelt betyr xm/n den n-te roten av x hevet til m-te potensen: xm/n = (ⁿ√x)m.
Spesielle eksponenter
- x⁰ = 1 for enhver ikke-null x (per definisjon).
- 1ⁿ = 1 for enhver eksponent n.
- 0ⁿ = 0 for enhver positiv eksponent n.
Bruksområder for eksponentiering
Eksponentiering brukes i mange felt som:
- Renteutregninger i finans
- Vitenskapelig notasjon for veldig store eller små tall
- Fysikk- og ingeniørformler
- Datavitenskap for algoritmisk kompleksitet
Viktige notater
- Negative baser med brøkeksponenter kan resultere i komplekse tall.
- Null hevet til en negativ eller null eksponent er udefinert.
CalcuLife.com
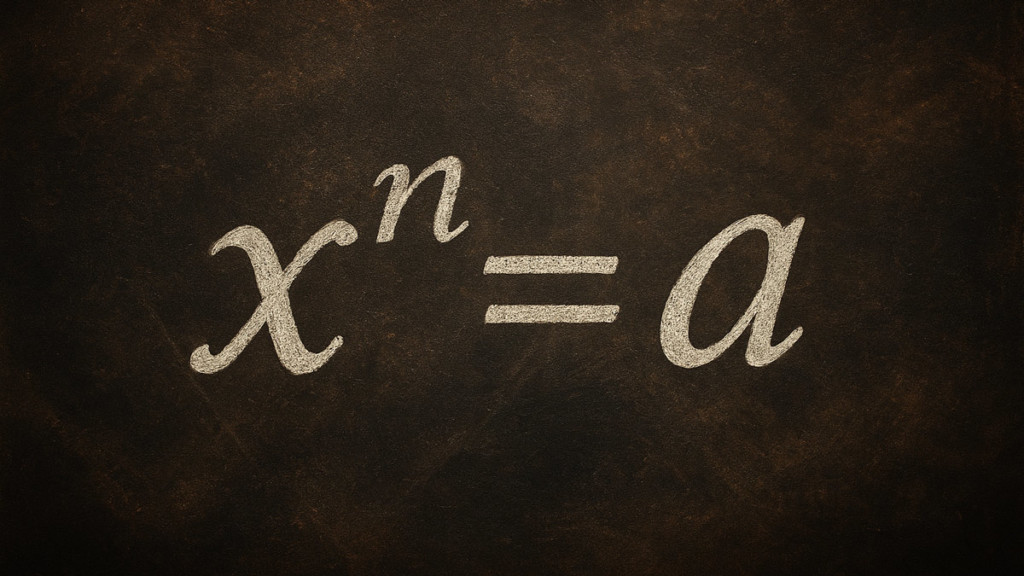








Legg igjen en kommentar