Our Arctan Calculator is a straightforward online tool designed for computing the arctangent of any given number. This calculator is especially useful for students, educators, and professionals who need to quickly determine the angle corresponding to a tangent value in trigonometry.
Arctan Calculator
Enter any value to calculate the arctangent.
How to Use the Calculator
Using the calculator is simple:
- Enter any number in the input field. There’s no restriction on the range of values you can input.
- Click ‘Calculate Arctan’ to get the arctangent of the entered value.
- The calculator will display the result in both degrees and radians.
- If you want to perform another calculation, click ‘Clear’ to reset the calculator.
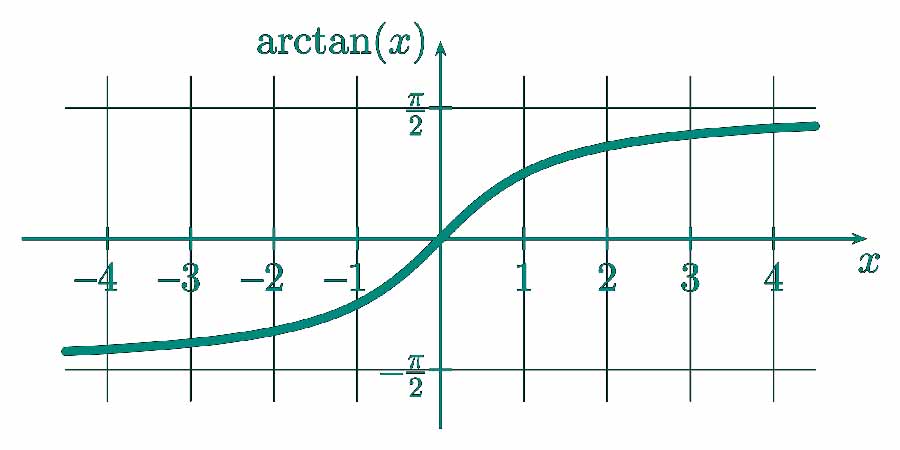
Understanding the Formula and Calculations
The arctan function, also known as tan⁻¹, is the inverse of the tangent function. It finds the angle whose tangent is the given number. The formula applied is:
- arctan(x) = tan⁻¹(x)
For any value ‘x’, arctan(x) returns the angle, typically measured in radians or degrees. The standard range for arctan is from -π/2 to π/2 radians (or -90° to 90° in degrees).
Educational Insights on Arctangent
The concept of arctan is fundamental in trigonometry and is pivotal in understanding the relationship between angles and the ratios of sides in right triangles. It’s essential in solving problems involving slopes, angles of elevation or depression, and in analyzing wave patterns in physics.
In real-world applications, arctan is vital in fields like engineering, where it helps in designing structures by calculating angles of support. In navigation and astronomy, it assists in determining positions and paths. Computer graphics and game development also utilize arctan in rendering 3D objects and calculating viewing angles.
Understanding arctan is crucial for anyone delving into fields involving geometry, physics, or any discipline where angles and their measurements are important. This calculator simplifies these complex calculations, making it easier to grasp and apply these concepts.
© CalcuLife.com






Leave A Comment