Máy Tính Lũy Thừa Trực Tuyến

Công cụ này tính toán giá trị của bất kỳ số nào được nâng lên một lũy thừa nhất định. Chỉ cần nhập một cơ sở và một số mũ, máy tính sẽ hiển thị kết quả cùng với các bước tính toán. Đây là công cụ lý tưởng cho sinh viên, kỹ sư và bất kỳ ai làm việc với lũy thừa, hỗ trợ cả số nguyên và số thập phân. Công cụ này đặc biệt hữu ích cho học sinh và sinh viên tại Việt Nam trong việc học toán và thực hành các bài tập liên quan đến lũy thừa.

Máy Tính Lũy Thừa

xⁿ = a

Số Cơ Sở (x)

Độ Lũy Thừa (n)

Kết Quả (a)

Quá trình tính toán sẽ xuất hiện ở đây.

Chia sẻ nội dung này?

Cách Sử Dụng Máy Tính Này

Nhập Cơ Sở (x): Nhập số mà bạn muốn nâng lên lũy thừa.
Nhập Số Mũ (n): Nhập lũy thừa mà cơ sở cần được nâng lên.
Xem Kết Quả (a): Kết quả sẽ được tính toán và hiển thị tự động.
Kiểm Tra Các Bước: Một phân tích chi tiết của phép tính sẽ xuất hiện dưới kết quả.
Sao Chép Kết Quả: Nhấn “Sao Chép Kết Quả” để lưu đầu ra vào clipboard của bạn.
Xóa: Nhấn “Xóa Tất Cả” để đặt lại tất cả các trường và bắt đầu một phép tính mới.

Bảng Giá Trị

x	x²	x³	x⁴	x⁵
1	1	1	1	1
2	4	8	16	32
3	9	27	81	243
4	16	64	256	1024
5	25	125	625	3125
6	36	216	1296	7776
7	49	343	2401	16807
8	64	512	4096	32768
9	81	729	6561	59049
10	100	1000	10000	100000

Hiểu Về Lũy Thừa

Lũy thừa là một phép toán toán học liên quan đến việc nâng một số cơ sở (x) lên lũy thừa của một số mũ (n). Nó được viết là xⁿ và có nghĩa là nhân cơ sở với chính nó n lần. Ví dụ, 3² = 3 × 3 = 9.

Khái Niệm Cơ Bản

Trong biểu thức xⁿ:

x là cơ sở — số được nhân.
n là số mũ — nó cho biết số lần cơ sở được nhân với chính nó.
a là kết quả — giá trị cuối cùng của phép toán.

Số Mũ Âm Là Gì?

Một số mũ âm có nghĩa là nghịch đảo của cơ sở được nâng lên lũy thừa dương đối diện. Ví dụ:

2⁻¹ = 1 / 2¹ = 1/2
3⁻² = 1 / (3²) = 1/9

Nói chung, x⁻ⁿ = 1 / xⁿ cho bất kỳ cơ sở x nào khác không bằng 0.

Số Mũ Thập Phân hoặc Phân Số Là Gì?

Số mũ thập phân hoặc phân số đại diện cho căn bậc. Ví dụ:

x^0.5 = √x (căn bậc hai của x)
x^0.25 = ⁴√x (căn bậc bốn của x)
x^1.5 = x × √x

Nói chung, x^m/n có nghĩa là căn bậc n của x được nâng lên lũy thừa m: x^m/n = (ⁿ√x)^m.

Các Số Mũ Đặc Biệt

x⁰ = 1 cho bất kỳ x nào khác không bằng 0 (theo định nghĩa).
1ⁿ = 1 cho bất kỳ số mũ n nào.
0ⁿ = 0 cho bất kỳ số mũ dương n nào.

Ứng Dụng Của Lũy Thừa

Lũy thừa được sử dụng trong nhiều lĩnh vực như:

Tính toán lãi suất kép trong tài chính
Ký hiệu khoa học cho các số rất lớn hoặc rất nhỏ
Các công thức vật lý và kỹ thuật
Khoa học máy tính cho độ phức tạp của thuật toán

Lưu Ý Quan Trọng

Các cơ sở âm với số mũ phân số có thể dẫn đến các số phức.
Không xác định khi 0 được nâng lên số mũ âm hoặc số mũ bằng 0.

CalcuLife.com

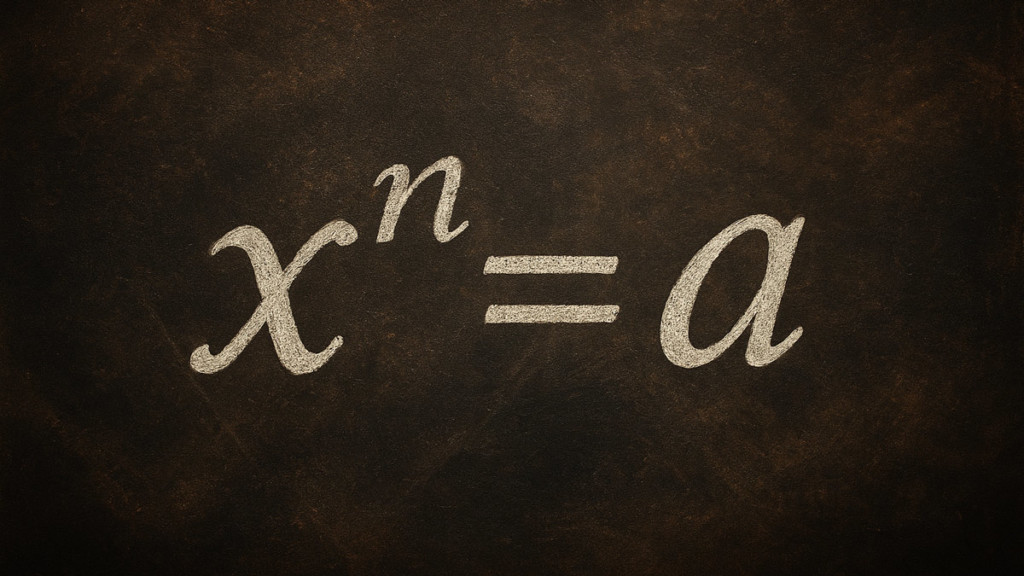
Máy Tính Lũy Thừa Trực Tuyến