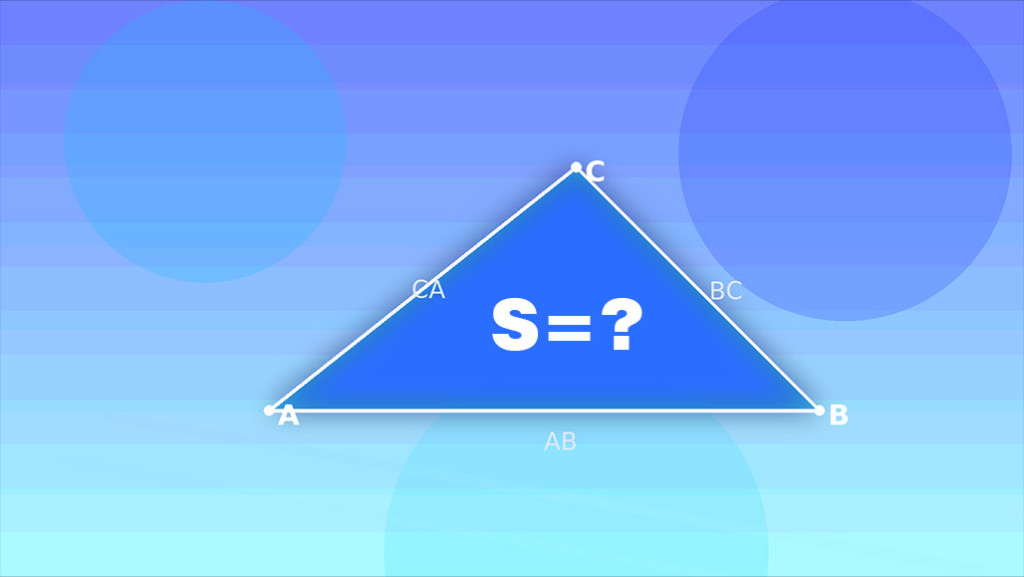
Online calculator for the area of a triangle from three side lengths (AB, BC, CA) using Heron’s formula. It checks triangle inequality, shows a proportional diagram with vertices A, B, C, and draws a clear “roof attempt” for impossible sets. The diagram keeps side lengths in correct visual proportion. Labels appear on edges (AB, BC, CA) and on vertices (A, B, C).
Triangle Area Calculator (3 Sides)
Enter side lengths AB, BC, CA. Area (S) is computed by Heron’s formula. The diagram keeps true proportions and labels A, B, C and sides AB, BC, CA. If the sides can’t form a triangle, a clear “roof attempt” with the gap is drawn and the result says “doesn’t exist”.
Side AB
Side BC
Side CA
Area (S)
How to Use
- Enter three positive side lengths for AB, BC, and CA.
- Press Calculate.
- Read the area S and review the working and diagram.
- Use Decimal Places to control rounding of the result and labels.
Notes: If the sides cannot form a triangle, the result shows “doesn’t exist” and the visualization draws the longest side as the base with two dashed arms that do not meet, highlighting the gap.
Use consistent units for all sides; the area will be in those units squared (m², cm², in², ft², etc.).
Formulas
Triangle inequality (existence): AB + BC > CA, AB + CA > BC, BC + CA > AB (all strict).
Semiperimeter: s = (AB + BC + CA) / 2
Heron’s formula (area): S = √[ s(s − AB)(s − BC)(s − CA) ]
- Equivalent form: S = (1/4) √[(AB + BC + CA)(−AB + BC + CA)(AB − BC + CA)(AB + BC − CA)].
- From area to height on AB: hAB = 2S / AB (similarly for other bases).
- With inradius r and circumradius R: S = r·s = (AB·BC·CA)/(4R).
- Equilateral (side a): S = (√3/4)·a².
Example Values
| AB | BC | CA | Valid? | Area S |
| 3 | 4 | 5 | Yes | 6 |
| 5 | 5 | 6 | Yes | 12 |
| 7 | 5 | 6 | Yes | 14.6969 |
| 8 | 8 | 8 | Yes | 27.7128 |
| 10 | 6 | 8 | Yes | 24 |
| 9 | 12 | 15 | Yes | 54 |
| 2.5 | 4 | 5 | Yes | 4.9525 |
| 12 | 13 | 5 | Yes | 30 |
| 20 | 13 | 7 | No | — |
| 6.5 | 6.5 | 4.2 | Yes | 12.918 |
| 15 | 14 | 9 | Yes | 61.6441 |
| 30 | 29 | 10 | Yes | 144.6373 |
| 100 | 120 | 150 | Yes | 5981.168 |
| 1.2 | 1.3 | 2.4 | Yes | 0.4196 |
| 9 | 9 | 18 | No | — |
Interesting Facts
- Heron’s result: The formula is attributed to Heron of Alexandria (1st century CE) and needs only side lengths, no angles or heights.
- Heronian triangles: Triangles with integer sides and integer area (e.g., 3-4-5 has S = 6) are called Heronian.
- Maximum area: For a fixed perimeter, the equilateral triangle has the largest area. For two fixed sides, area is maximized when the included angle is 90°.
- Degeneracy: When one sum equals the third side (e.g., 20, 13, 7), the “triangle” collapses to a segment and S = 0.
- Checks: From S and a base, heights, inradius (r = S/s), and circumradius (R = AB·BC·CA/(4S)) are directly recoverable.
CalcuLife.com







Leave A Comment