Deze tool berekent de waarde van elk getal dat tot een bepaalde macht wordt verheven. Voer eenvoudig een basis en een exponent in, en de calculator toont het resultaat samen met de berekeningsstappen. Ideaal voor studenten, ingenieurs en iedereen die met machten werkt, ondersteunt deze tool zowel gehele getallen als decimalen. Dit soort hulpmiddelen is bijzonder nuttig voor de Nederlandse onderwijssector, waar wiskunde een belangrijk onderdeel van het curriculum is.
Exponentiële Calculator
xn = a
Basisgetal (x)
Exponent (n)
Resultaat (a)
Hoe deze calculator te gebruiken
- Voer Basis (x) in: Typ het getal dat je tot een macht wilt verheffen.
- Voer Exponent (n) in: Typ de macht waartoe de basis moet worden verheven.
- Bekijk Resultaat (a): Het resultaat wordt automatisch berekend en weergegeven.
- Controleer Stappen: Een uitsplitsing van de berekening verschijnt onder het resultaat.
- Kopieer Resultaat: Klik op “Kopieer Resultaat” om de uitvoer naar je klembord op te slaan.
- Wis: Klik op “Wis Alles” om alle velden te resetten en een nieuwe berekening te starten.
Tabel van Waarden
| x | x² | x³ | x⁴ | x⁵ |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 4 | 8 | 16 | 32 |
| 3 | 9 | 27 | 81 | 243 |
| 4 | 16 | 64 | 256 | 1024 |
| 5 | 25 | 125 | 625 | 3125 |
| 6 | 36 | 216 | 1296 | 7776 |
| 7 | 49 | 343 | 2401 | 16807 |
| 8 | 64 | 512 | 4096 | 32768 |
| 9 | 81 | 729 | 6561 | 59049 |
| 10 | 100 | 1000 | 10000 | 100000 |
Exponentiatie Begrijpen
Exponentiatie is een wiskundige bewerking waarbij een basisgetal (x) tot de macht van een exponent (n) wordt verheven. Het wordt geschreven als xⁿ en betekent dat de basis n keer met zichzelf wordt vermenigvuldigd. Bijvoorbeeld, 3² = 3 × 3 = 9.
Basisconcept
In de uitdrukking xⁿ:
- x is de basis — het getal dat wordt vermenigvuldigd.
- n is de exponent — het geeft aan hoe vaak de basis met zichzelf wordt vermenigvuldigd.
- a is het resultaat — de uiteindelijke waarde van de bewerking.
Wat is een Negatieve Exponent?
Een negatieve exponent betekent de reciproke van de basis verheven tot de tegenovergestelde positieve macht. Bijvoorbeeld:
- 2⁻¹ = 1 / 2¹ = 1/2
- 3⁻² = 1 / (3²) = 1/9
In het algemeen geldt x⁻ⁿ = 1 / xⁿ voor elke niet-nul basis x.
Wat is een Decimale of Breuk Exponent?
Decimale of breuk exponenten vertegenwoordigen wortels. Bijvoorbeeld:
- x0.5 = √x (vierkantswortel van x)
- x0.25 = ⁴√x (vierde wortel van x)
- x1.5 = x × √x
In het algemeen betekent xm/n de n-de wortel van x verheven tot de m-de macht: xm/n = (ⁿ√x)m.
Speciale Exponenten
- x⁰ = 1 voor elke niet-nul x (per definitie).
- 1ⁿ = 1 voor elke exponent n.
- 0ⁿ = 0 voor elke positieve exponent n.
Toepassingen van Exponentiatie
Exponentiatie wordt in veel gebieden gebruikt, zoals:
- Samengestelde rente berekeningen in de financiën
- Wetenschappelijke notatie voor zeer grote of kleine getallen
- Fysica en techniek formules
- Informatica voor algoritmecomplexiteit
Belangrijke Opmerkingen
- Negatieve bases met breuk exponenten kunnen resulteren in complexe getallen.
- Zero verheven tot een negatieve of nul exponent is niet gedefinieerd.
CalcuLife.com
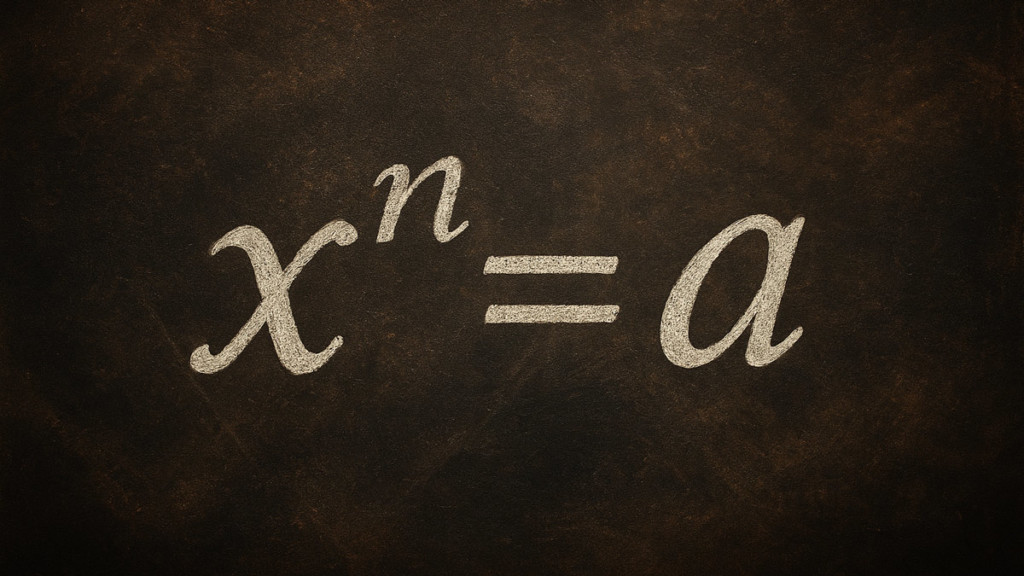






Laat een reactie achter