Dieses Tool berechnet den Wert einer Zahl, die mit einem bestimmten Exponenten potenziert wird. Gib einfach eine Basis und einen Exponenten ein, und der Rechner zeigt das Ergebnis zusammen mit den Rechenschritten an. Ideal für Schüler, Ingenieure und alle, die mit Potenzen arbeiten – unterstützt sowohl ganze Zahlen als auch Dezimalzahlen.
Potenzrechner
xn = a
Basiszahl (x)
Exponent (n)
Ergebnis (a)
So verwendest du diesen Rechner
- Basis eingeben (x): Gib die Zahl ein, die potenziert werden soll.
- Exponent eingeben (n): Gib den Exponenten ein, mit dem die Basis potenziert werden soll.
- Ergebnis ansehen (a): Das Ergebnis wird automatisch berechnet und angezeigt.
- Schritte überprüfen: Die Rechenschritte erscheinen unter dem Ergebnis.
- Ergebnis kopieren: Klicke auf „Ergebnis kopieren“, um den Wert in die Zwischenablage zu kopieren.
- Löschen: Klicke auf „Alles löschen“, um alle Felder zurückzusetzen und neu zu starten.
Wertetabelle
| x | x² | x³ | x⁴ | x⁵ |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 4 | 8 | 16 | 32 |
| 3 | 9 | 27 | 81 | 243 |
| 4 | 16 | 64 | 256 | 1024 |
| 5 | 25 | 125 | 625 | 3125 |
| 6 | 36 | 216 | 1296 | 7776 |
| 7 | 49 | 343 | 2401 | 16807 |
| 8 | 64 | 512 | 4096 | 32768 |
| 9 | 81 | 729 | 6561 | 59049 |
| 10 | 100 | 1000 | 10000 | 100000 |
Exponentiation verstehen
Potenzieren ist eine mathematische Operation, bei der eine Basiszahl (x) mit einem Exponenten (n) potenziert wird. Man schreibt es als xⁿ und es bedeutet, dass die Basis n-mal mit sich selbst multipliziert wird. Zum Beispiel: 3² = 3 × 3 = 9.
Grundprinzip
In dem Ausdruck xⁿ:
- x ist die Basis – die Zahl, die multipliziert wird.
- n ist der Exponent – er gibt an, wie oft die Basis multipliziert wird.
- a ist das Ergebnis – der Endwert der Berechnung.
Was ist ein negativer Exponent?
Ein negativer Exponent bedeutet den Kehrwert der Basis mit positivem Exponenten. Zum Beispiel:
- 2⁻¹ = 1 / 2¹ = 1/2
- 3⁻² = 1 / (3²) = 1/9
Allgemein gilt: x⁻ⁿ = 1 / xⁿ für jede Basis x ≠ 0.
Was ist ein Dezimal- oder Bruch-Exponent?
Dezimal- oder Bruch-Exponenten stehen für Wurzeln. Zum Beispiel:
- x0.5 = √x (Quadratwurzel von x)
- x0.25 = ⁴√x (vierte Wurzel von x)
- x1.5 = x × √x
Allgemein gilt: xm/n bedeutet die n-te Wurzel von x zur m-ten Potenz: xm/n = (ⁿ√x)m.
Spezielle Potenzen
- x⁰ = 1 für alle x ≠ 0 (Definition).
- 1ⁿ = 1 für jeden Exponenten n.
- 0ⁿ = 0 für n > 0.
Anwendungen der Potenzrechnung
Potenzrechnung wird in vielen Bereichen verwendet, z. B.:
- Zinseszins-Berechnungen in der Finanzwelt
- Wissenschaftliche Notation für sehr große oder kleine Zahlen
- Physik- und Ingenieurformeln
- Informatik, z. B. für Komplexitätsanalysen
Wichtige Hinweise
- Negative Basen mit Bruch-Exponenten können komplexe Zahlen ergeben.
- 0 mit negativem oder null Exponenten ist nicht definiert.
CalcuLife.com
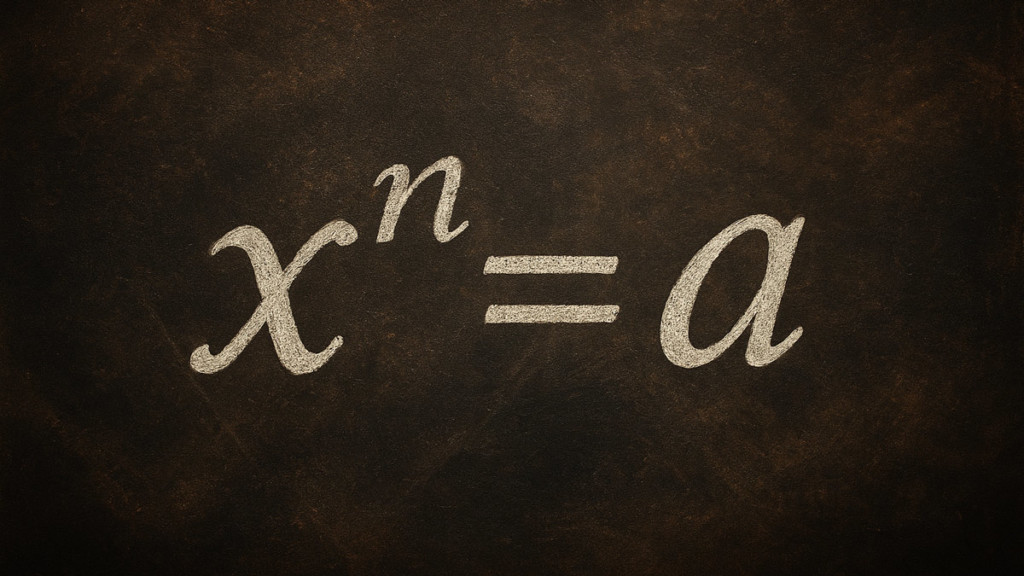






Hinterlasse einen Kommentar