Онлайн калькулятор арккосинуса – Обратный косинус

Используйте этот калькулятор арккосинуса (обратного косинуса), чтобы получить главный угол θ из значения косинуса x. Математика, лежащая в основе инструмента, следует стандартному определению обратных круговых функций, как это задокументировано в Цифровой библиотеке математических функций NIST (см. Обратные круговые функции на dlmf.nist.gov/4.23).

Поделиться этим?

Копировать ссылку ✓

Как работает калькулятор арккосинуса

1. Вы вводите число x в диапазоне от −1 до 1.
2. Инструмент вычисляет θ = арккос(x) как главное значение в радианах, затем показывает и градусы.
3. Он также отображает sin(θ) и чистую визуализацию единичной окружности с радиусом, проекциями и точкой.

Определение и формула

Арккос возвращает главный угол θ, который удовлетворяет условию cos(θ) = x.

• Область допустимых значений: x ∈ [−1, 1]
• Диапазон выходных значений (главное значение): θ ∈ [0, π] радиан, что соответствует [0°, 180°]
• Преобразование: градусы = радианы × 180/π

Ключевая идентичность: если cos(θ) = x, то θ = арккос(x). Для углов вне главного диапазона существуют другие решения: 2π − θ и т.д. Этот инструмент по замыслу сообщает главное значение.

Входные данные, выходные данные и точность

• Допустимый ввод x: любое действительное число от −1 до 1. Значения вне этого диапазона не определены для действительных углов.
• Форматы углов: инструмент показывает как градусы, так и радианы.
• Десятичные знаки: используйте элемент управления «Десятичные знаки», чтобы установить округление (0–10). Радианы часто требуют 4–6 десятичных знаков; градусы обычно хорошо воспринимают 2–4.

Быстрые примеры

• x = 1 → θ = 0 рад = 0°
• x = 0.5 → θ = арккос(0.5) = π/3 ≈ 1.0472 рад ≈ 60°
• x = 0 → θ = π/2 ≈ 1.5708 рад ≈ 90°
• x = −1 → θ = π ≈ 3.1416 рад = 180°

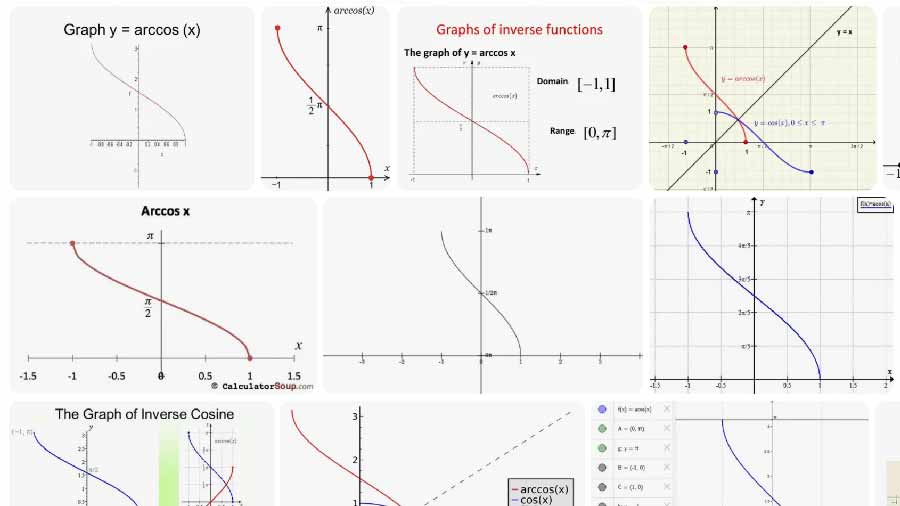
Интерпретация единичной окружности

На единичной окружности (радиус 1) x является прилежащей стороной прямоугольного треугольника, построенного от положительной оси x до точки на окружности, а √(1 − x²) — противолежащей стороной. Арккос возвращает угол θ, который помещает точку в (x, √(1 − x²)) на верхней полукруге или (x, 0) на концах. Холст показывает радиус до этой точки и пунктирные проекции на оси.

Распространенные применения арккос

• Угол между векторами: для нормализованных векторов u и v, u·v = cos(θ) ⇒ θ = арккос(u·v).
• Геометрия и треугольники: восстановление угла по длинам сторон с помощью теоремы косинусов.
• Робототехника и 3D графика: преобразование скалярных произведений в углы для расчетов освещения, камеры и позы.
• Обработка сигналов: фазовые соотношения и углы корреляции.

Заметки по точности и округлению

• Ввод с плавающей точкой, близкий к ±1, может усиливать шум округления. Если появляется значение, например, 1.0000001, ограничьте его до 1 для стабильного результата.
• Радианы имеют точные простые формы для специальных углов (π/3, π/2, π). Десятичный дисплей будет показывать округленные приближения.
• Если вам нужна максимальная точность, увеличьте элемент управления десятичными знаками и прочитайте значение в радианах.

Часто задаваемые вопросы

Является ли арккос тем же, что и cos⁻¹?
Да. cos⁻¹(x) означает обратную функцию арккос(x), а не 1/cos(x).

Почему калькулятор отклоняет значения меньше −1 или больше 1?
Для действительных углов косинус ограничен диапазоном [−1, 1]. Входные данные вне этого интервала не имеют действительного арккос.

Почему я получаю только один угол?
Калькулятор возвращает главное значение в [0, π]. Существуют другие котерминальные или дополнительные углы, но главная ветвь является стандартной для обратных тригонометрических функций и сохраняет результаты предсказуемыми.

Следует ли использовать градусы или радианы?
Используйте градусы для повседневного понимания и радианы для вычислений, физики и большинства библиотек программирования.

Как вы используете этот калькулятор? Хотели бы вы другие инструменты или функции? Дайте нам знать в комментариях!

CalcuLife.com