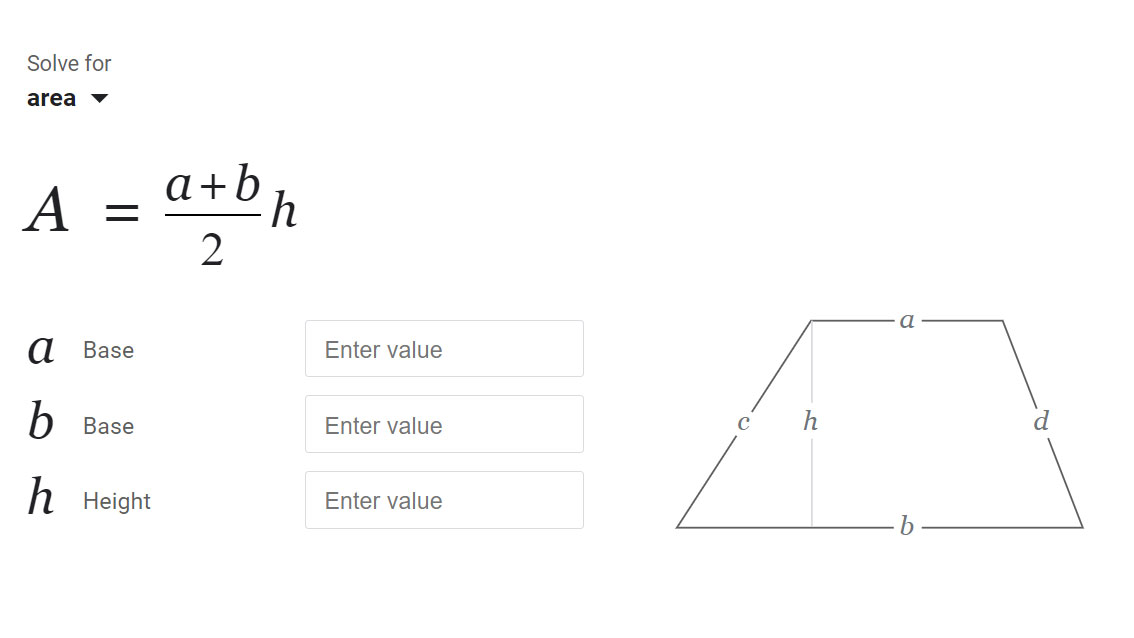
Trapezoid Area Calculator finds the area of a trapezoid from its two bases and height using the standard geometry formula. The only inputs you need are the lengths of the top base a, the bottom base b, and the perpendicular height h. The visualization centers and scales to your numbers so you can see which side is which.
How the calculator works
- Inputs: Top base a, bottom base b, height h (all positive real numbers).
- Formula:
Area = ((a + b) / 2) × h. For a concise reference on the formula, see Wolfram MathWorld: Trapezoid. - Units: The output is in square units. If inputs are in meters, the result is in m²; if in inches, in in². The tool leaves units generic to fit any context.
- Visualization: The diagram always stays centered in the canvas and labels the same quantities you typed: a across the top, b across the bottom, and h as the perpendicular distance between them.
- Numerical stability: The tool accepts decimals, large values, and small values. It rounds the display cleanly while keeping internal precision.
Why this formula is correct
A trapezoid’s area equals the height times the average of the two parallel sides. Intuitively, if you “slide” the short base along the height, you can rearrange the trapezoid into a rectangle whose width is the average of the two bases. That gives A = h × (a + b)/2.
Step-by-step examples
- Example 1 (matches the default drawing):
- a = 6, b = 10, h = 4
- Average of bases = (6 + 10)/2 = 8
- Area = 8 × 4 = 32 square units
- Example 2 (decimals):
- a = 3.5, b = 12, h = 2.8
- Average of bases = (3.5 + 12)/2 = 7.75
- Area = 7.75 × 2.8 = 21.7 square units
- Example 3 (skinny height):
- a = 20, b = 24, h = 0.5
- Average of bases = 22
- Area = 22 × 0.5 = 11 square units
Reverse calculations you might need
- Solve for height given area and bases:
h = (2 × Area) / (a + b) - Solve for an unknown base given area, the other base, and height:
a = (2 × Area) / h − b(or swap a and b)
What counts as the height
Height is perpendicular to the bases. It is not the slanted side. If the sides lean, the height is still the shortest straight distance between the two bases. In right or isosceles trapezoids this is easy to see; in obtuse cases it remains perpendicular.
Quality checks and edge cases
- Positivity: All three inputs must be greater than zero to produce an area.
- Equal bases: If a = b, the trapezoid becomes a rectangle; the formula reduces to
A = b × h, as expected. - Very large or very small numbers: Area scales linearly with height and with the average of the bases. Doubling every input doubles the area for height and doubles for bases’ average as appropriate.
Real-world trapezoid shapes
- Road cross-sections and medians: Shoulders and embankments often form trapezoids when viewed from the side.
- Roof framing: Some hip or shed-roof panels, and fascia profiles, are trapezoidal.
- Landscaping beds and ramps: Plan views and side profiles frequently yield trapezoids.
- Sheet-metal parts and tiles: Trapezoid blanks are common in manufacturing and flooring layouts.
- Trenches and channels: Engineering cross-sections of ditches often use trapezoidal profiles.
Using the result
- Materials estimation: Multiply area by thickness to approximate volume (e.g., soil or concrete). Keep unit consistency.
- Costing: If a material is priced per square unit, multiply the unit cost by your area to estimate spend.
- Scaling drawings: If your inputs came from a scaled plan, convert to real-world units before calculating area.
Common mistakes to avoid
- Using a slanted side instead of the perpendicular height.
- Adding units incorrectly. Keep all inputs in the same unit so the output is in square of that unit.
- Forgetting that the formula uses the average of the bases, not their difference.
CalcuLife.com





Leave A Comment