Calculadora Arccos Online – Cosseno Inverso

Use esta calculadora de Arccos (cosseno inverso) para obter o ângulo principal θ a partir de um valor de cosseno x. A matemática por trás da ferramenta segue a definição padrão das funções circulares inversas, conforme documentado pela Biblioteca Digital de Funções Matemáticas do NIST (veja Funções Circulares Inversas em dlmf.nist.gov/4.23).

Compartilhar isto?

Copiar link ✓

Como a calculadora de arccos funciona

1. Você insere um número x entre −1 e 1.
2. A ferramenta calcula θ = arccos(x) como o valor principal em radianos e também mostra em graus.
3. Ela também exibe sin(θ) e uma visualização limpa do círculo unitário com o raio, projeções e ponto.

Definição e fórmula

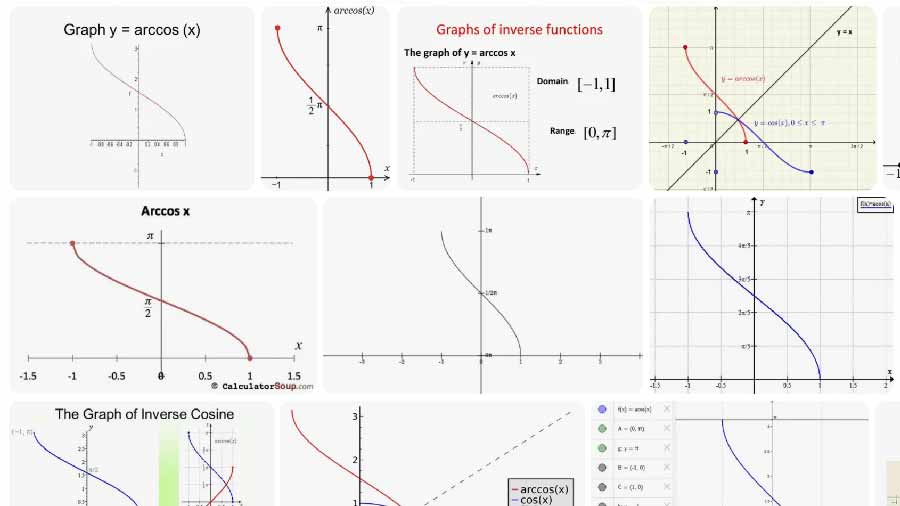
Arccos retorna o ângulo principal θ que satisfaz cos(θ) = x.

• Domínio de entrada: x ∈ [−1, 1]
• Intervalo de saída (valor principal): θ ∈ [0, π] radianos, que é [0°, 180°]
• Conversão: graus = radianos × 180/π

Identidade chave: se cos(θ) = x, então θ = arccos(x). Para ângulos fora do intervalo principal, existem outras soluções: 2π − θ, etc. Esta ferramenta reporta o valor principal por design.

Entradas, saídas e precisão

• Entrada válida x: qualquer número real de −1 a 1. Valores fora desse intervalo são indefinidos para ângulos reais.
• Formatos de ângulo: a ferramenta mostra tanto em graus quanto em radianos.
• Casas decimais: use o controle “Casas Decimais” para definir o arredondamento (0–10). Radianos geralmente se beneficiam de 4–6 casas decimais; graus costumam estar bem com 2–4.

Exemplos rápidos

• x = 1 → θ = 0 rad = 0°
• x = 0,5 → θ = arccos(0,5) = π/3 ≈ 1,0472 rad ≈ 60°
• x = 0 → θ = π/2 ≈ 1,5708 rad ≈ 90°
• x = −1 → θ = π ≈ 3,1416 rad = 180°

Interpretação do círculo unitário

No círculo unitário (raio 1), x é o lado adjacente do triângulo retângulo construído a partir do eixo x positivo até o ponto no círculo, e √(1 − x²) é o lado oposto. Arccos retorna o ângulo θ que coloca o ponto em (x, √(1 − x²)) na semicircunferência superior ou (x, 0) nos extremos. A tela mostra o raio até esse ponto e projeções tracejadas nos eixos.

Usos comuns do arccos

• Ângulo entre vetores: com vetores normalizados u e v, u·v = cos(θ) ⇒ θ = arccos(u·v).
• Geometria e triângulos: recuperar um ângulo a partir dos comprimentos dos lados via a Lei dos Cossenos.
• Robótica e gráficos 3D: converter produtos escalares em ângulos para cálculos de iluminação, câmera e pose.
• Processamento de sinais: relações de fase e ângulos de correlação.

Notas sobre precisão e arredondamento

• A entrada em ponto flutuante próxima a ±1 pode amplificar o ruído de arredondamento. Se um valor como 1,0000001 aparecer, limite-o a 1 para um resultado estável.
• Radianos possuem formas exatas simples para ângulos especiais (π/3, π/2, π). A exibição decimal mostrará aproximações arredondadas.
• Se você precisar de máxima precisão, aumente o controle de casas decimais e leia o valor em radianos.

Perguntas Frequentes

O arccos é o mesmo que cos⁻¹?
Sim. cos⁻¹(x) significa a função inversa arccos(x), não 1/cos(x).

Por que a calculadora rejeita valores menores que −1 ou maiores que 1?
Para ângulos reais, o cosseno é limitado a [−1, 1]. Entradas fora desse intervalo não têm arccos real.

Por que eu só obtenho um ângulo?
A calculadora retorna o valor principal em [0, π]. Outros ângulos coterminais ou suplementares existem, mas o ramo principal é padrão para funções trigonométricas inversas e mantém os resultados previsíveis.

Devo usar graus ou radianos?
Use graus para interpretação do dia a dia e radianos para cálculo, física e a maioria das bibliotecas de programação.

Qual é o seu caso de uso desta calculadora? Você gostaria de outras ferramentas ou recursos? Deixe-nos saber nos comentários!

CalcuLife.com