이 도구는 주어진 거듭제곱으로 어떤 숫자의 값을 계산합니다. 기본값과 지수를 입력하면 계산기가 결과와 함께 계산 단계를 표시합니다. 학생, 엔지니어 및 거듭제곱을 다루는 모든 사람에게 이상적이며, 이 도구는 정수와 소수를 모두 지원합니다. 이 도구는 한국의 교육 시스템에서도 유용하게 사용될 수 있습니다.
거듭제곱 계산기
xn = a
밑수 (x)
지수 (n)
결과 (a)
계산 과정이 여기에 표시됩니다.
이 계산기를 사용하는 방법
- 기본값 입력 (x): 거듭제곱할 숫자를 입력하세요.
- 지수 입력 (n): 기본값이 거듭제곱될 값을 입력하세요.
- 결과 보기 (a): 결과가 자동으로 계산되어 표시됩니다.
- 단계 확인: 결과 아래에 계산의 세부 사항이 나타납니다.
- 결과 복사: “결과 복사”를 클릭하여 출력을 클립보드에 저장하세요.
- 지우기: “모두 지우기”를 클릭하여 모든 필드를 초기화하고 새 계산을 시작하세요.
값의 표
| x | x² | x³ | x⁴ | x⁵ |
| 1 | 1 | 1 | 1 | 1 |
| 2 | 4 | 8 | 16 | 32 |
| 3 | 9 | 27 | 81 | 243 |
| 4 | 16 | 64 | 256 | 1024 |
| 5 | 25 | 125 | 625 | 3125 |
| 6 | 36 | 216 | 1296 | 7776 |
| 7 | 49 | 343 | 2401 | 16807 |
| 8 | 64 | 512 | 4096 | 32768 |
| 9 | 81 | 729 | 6561 | 59049 |
| 10 | 100 | 1000 | 10000 | 100000 |
거듭제곱 이해하기
거듭제곱은 기본 숫자(x)를 지수(n)의 거듭제곱으로 올리는 수학적 연산입니다. 이는 xⁿ으로 표기되며, 기본값을 n번 곱하는 것을 의미합니다. 예를 들어, 3² = 3 × 3 = 9입니다.
기본 개념
표현식 xⁿ에서:
- x는 기본값 — 곱해지는 숫자입니다.
- n은 지수 — 기본값이 자신과 몇 번 곱해지는지를 나타냅니다.
- a는 결과 — 연산의 최종 값입니다.
음수 지수란 무엇인가요?
음수 지수는 기본값을 반대의 양수 거듭제곱으로 올린 역수를 의미합니다. 예를 들어:
- 2⁻¹ = 1 / 2¹ = 1/2
- 3⁻² = 1 / (3²) = 1/9
일반적으로 x⁻ⁿ = 1 / xⁿ는 어떤 비영(非零) 기본값 x에 대해 성립합니다.
소수 또는 분수 지수란 무엇인가요?
소수 또는 분수 지수는 루트를 나타냅니다. 예를 들어:
- x0.5 = √x (x의 제곱근)
- x0.25 = ⁴√x (x의 네 번째 제곱근)
- x1.5 = x × √x
일반적으로 xm/n는 x의 n번째 제곱근을 m번째 거듭제곱으로 올리는 것을 의미합니다: xm/n = (ⁿ√x)m.
특별한 지수
- x⁰ = 1는 어떤 비영(非零) x에 대해 성립합니다 (정의에 의해).
- 1ⁿ = 1는 어떤 지수 n에 대해 성립합니다.
- 0ⁿ = 0는 어떤 양수 지수 n에 대해 성립합니다.
거듭제곱의 응용
거듭제곱은 다음과 같은 여러 분야에서 사용됩니다:
- 금융에서의 복리 계산
- 매우 크거나 작은 숫자를 위한 과학적 표기법
- 물리학 및 공학 공식
- 알고리즘 복잡성을 위한 컴퓨터 과학
중요한 주의 사항
- 분수 지수를 가진 음수 기본값은 복소수를 초래할 수 있습니다.
- 제로를 음수 또는 제로 지수로 올리는 것은 정의되지 않습니다.
CalcuLife.com
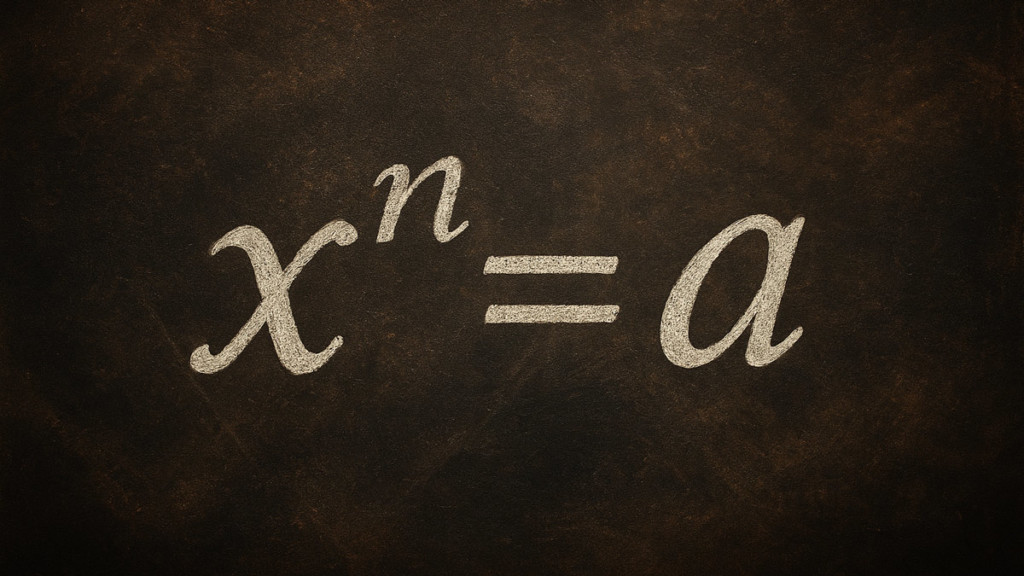







댓글 남기기