Transformez toute entrée en degrés (°) en radians (rad) avec un facteur exact basé sur les normes. Conçu pour le travail en trigonométrie, les rotations CAD/CAM, les moteurs de jeu, les articulations de robotique et les fiches techniques qui nécessitent des unités d’angle SI. Cet outil est particulièrement utile pour les étudiants et les professionnels en France qui travaillent avec des calculs d’angles.
Convertisseur de Degrés (°) en Radians (rad)
Entrez une valeur dans le champ ci-dessous et appuyez sur le bouton
Degrés (°)
Résultat en Radians (rad)
Étapes rapides
- Entrez un angle en degrés.
- Choisissez le nombre de décimales que vous souhaitez.
- Sélectionnez Convertir pour obtenir les radians et la ligne de calcul.
- Copiez le résultat pour placer le nombre dans votre presse-papiers.
- Effacer tout pour réinitialiser.
- Utilisez Échanger si vous avez besoin de la calculatrice inverse.
Unités, précisément
Degré (°) — Unité non-SI de l’angle plan. Une révolution complète contient 360 degrés, donc un degré équivaut à π/180 d’un tour. Abréviation : °. Système : non-SI. Relation exacte utilisée dans cet outil : 1° = π/180 rad ≈ 0.01745329252 rad.
Radian (rad) — Unité SI de l’angle plan définie par la longueur de l’arc égale au rayon d’un cercle. Une révolution complète contient 2π radians. Abréviation : rad. Système : SI. Relation exacte utilisée dans cet outil : 1 rad = 180/π° ≈ 57.29577951°.
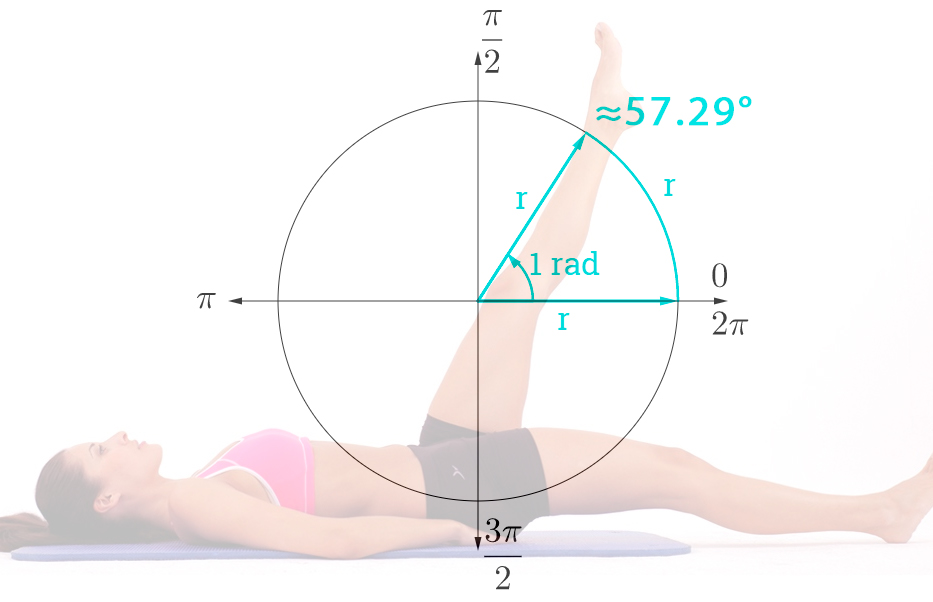Voici à quoi ressemble un radian sur un cercle
Formule et source
radians = degrés × π ÷ 180
Source : NIST
Tableau de correspondance
| Degrés (°) | Exact en π | Radians |
|---|---|---|
| 0 | 0 | 0.000000 |
| 15 | π/12 | 0.261799 |
| 18 | π/10 | 0.314159 |
| 22.5 | π/8 | 0.392699 |
| 30 | π/6 | 0.523599 |
| 45 | π/4 | 0.785398 |
| 60 | π/3 | 1.047198 |
| 75 | 5π/12 | 1.308997 |
| 90 | π/2 | 1.570796 |
| 120 | 2π/3 | 2.094395 |
| 135 | 3π/4 | 2.356194 |
| 150 | 5π/6 | 2.617994 |
| 180 | π | 3.141593 |
| 210 | 7π/6 | 3.665191 |
| 225 | 5π/4 | 3.926991 |
| 240 | 4π/3 | 4.188790 |
| 270 | 3π/2 | 4.712389 |
| 300 | 5π/3 | 5.235988 |
| 330 | 11π/6 | 5.759587 |
| 360 | 2π | 6.283185 |
Références concrètes
- Angle droit (angle droit) : 90° = 1.570796 rad
- Ligne droite (angle plat) : 180° = 3.141593 rad
- Tour complet (révolution) : 360° = 6.283185 rad
- Angle intérieur d’un triangle équilatéral : 60° = 1.047198 rad
- Angle intérieur d’un hexagone régulier : 120° = 2.094395 rad
- Angle central d’un pentagone régulier : 72° = 1.256637 rad
- Angle central d’un octogone régulier : 45° = 0.785398 rad
- Clic de l’horloge entre les marques de minute adjacentes : 6° = 0.104720 rad
- Angle de flanc de filetage ISO métrique : 60° = 1.047198 rad
- Angle inclus du filetage ACME : 29° = 0.506146 rad
Si vous le souhaitez, dites-nous comment vous utilisez cette calculatrice. Si un autre outil en ligne pourrait aider votre travail ou vos études, veuillez le mentionner dans les commentaires et nous envisagerons avec plaisir de le créer.
CalcuLife.com
Laisser un commentaire