Notre calculateur de cotangente est un outil en ligne pratique conçu pour calculer la cotangente d’un angle en degrés. Cet outil est particulièrement bénéfique pour les personnes qui effectuent des calculs trigonométriques en mathématiques, en physique et dans divers domaines de l’ingénierie. En France, où les mathématiques et la physique sont des matières clés dans l’éducation, cet outil peut s’avérer très utile pour les étudiants et les professionnels.
Calculateur de Cotangente
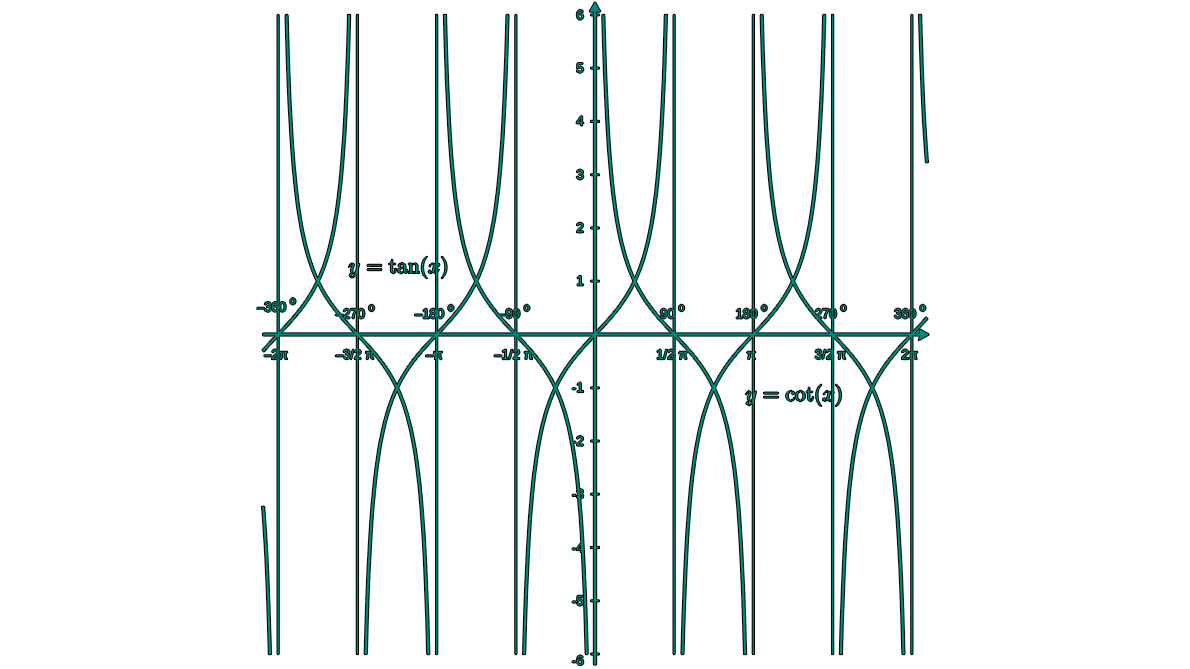
Comparaison des graphiques tg et cot
Comment utiliser le calculateur
Le calculateur de cotangente est simple et convivial :
- Entrez l’angle souhaité en degrés dans le champ de saisie du calculateur.
- Cliquez sur ‘Calculer la cotangente’ pour obtenir la valeur de la cotangente de l’angle.
- Le résultat affichera la cotangente de l’angle saisi.
- Pour effectuer un autre calcul, cliquez sur ‘Effacer’ pour réinitialiser le calculateur.
Comprendre la fonction cotangente
La cotangente est une fonction trigonométrique qui est l’inverse de la tangente. Elle est définie pour un angle dans un triangle rectangle comme le rapport du côté adjacent au côté opposé. La formule utilisée est :
- cotangente(θ) = 1 / tangente(θ)
Où θ est l’angle en degrés. Le calculateur convertit l’angle en radians pour le calcul, car les fonctions trigonométriques dans les langages de programmation utilisent généralement des radians.
Perspectives éducatives sur la cotangente
La cotangente est cruciale en trigonométrie pour comprendre les relations entre les angles et les côtés des triangles. Elle est particulièrement utile dans les applications impliquant des processus périodiques et des oscillations, comme dans les domaines de la physique et de l’ingénierie.
Dans des scénarios pratiques, la cotangente est utilisée en topographie pour les mesures de terrain, en navigation pour calculer des angles et des distances, et en architecture pour concevoir des structures. Une compréhension approfondie de la cotangente et de son application peut bénéficier considérablement aux étudiants et aux professionnels dans les disciplines scientifiques et techniques.
© CalcuLife.com






Laisser un commentaire