Online kalkulačka Arccos – Inverzní kosinus

Použijte tento kalkulátor Arccos (inverzní kosinus) k získání hlavního úhlu θ z hodnoty kosinu x. Matematika za tímto nástrojem vychází ze standardní definice inverzních obvodových funkcí, jak je zdokumentováno v Digitální knihovně matematických funkcí NIST (viz Inverzní obvodové funkce na dlmf.nist.gov/4.23).

Sdílet tohle?

Kopírovat odkaz ✓

Jak funguje kalkulátor arccos

1. Zadáte číslo x mezi −1 a 1.
2. Nástroj vypočítá θ = arccos(x) jako hlavní hodnotu v radiánech a také zobrazí stupně.
3. Také zobrazuje sin(θ) a čistou vizualizaci jednotkového kruhu s poloměrem, projekcemi a bodem.

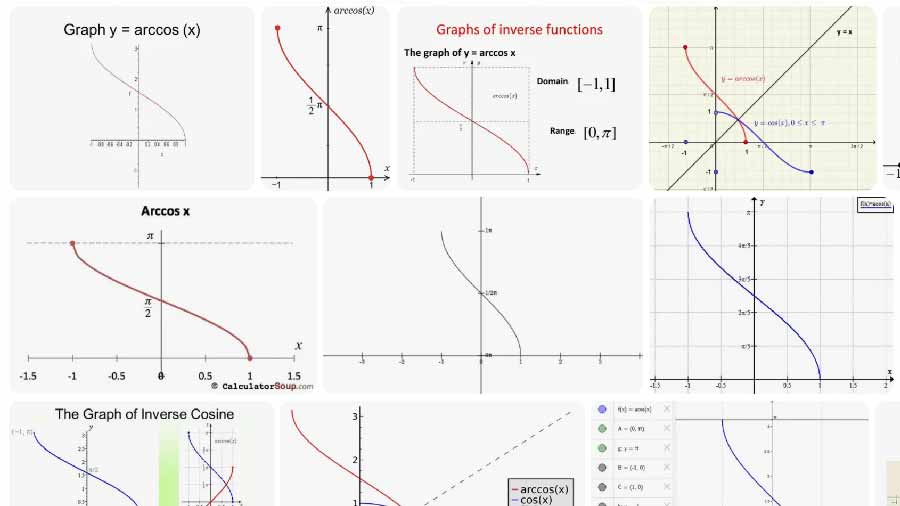
Definice a vzorec

Arccos vrací hlavní úhel θ, který splňuje cos(θ) = x.

• Vstupní doména: x ∈ [−1, 1]
• Výstupní rozsah (hlavní hodnota): θ ∈ [0, π] radiánů, což je [0°, 180°]
• Převod: stupně = radiány × 180/π

Klíčová identita: pokud cos(θ) = x, pak θ = arccos(x). Pro úhly mimo hlavní rozsah existují další řešení: 2π − θ atd. Tento nástroj hlásí hlavní hodnotu záměrně.

Vstupy, výstupy a přesnost

• Platný vstup x: jakékoli reálné číslo od −1 do 1. Hodnoty mimo tento rozsah nejsou definovány pro reálné úhly.
• Formáty úhlů: nástroj zobrazuje jak stupně, tak radiány.
• Desetinná místa: použijte ovládání „Desetinná místa“ pro nastavení zaokrouhlení (0–10). Radiány často těží z 4–6 desetinných míst; stupně jsou obvykle v pořádku s 2–4.

Rychlé příklady

• x = 1 → θ = 0 rad = 0°
• x = 0.5 → θ = arccos(0.5) = π/3 ≈ 1.0472 rad ≈ 60°
• x = 0 → θ = π/2 ≈ 1.5708 rad ≈ 90°
• x = −1 → θ = π ≈ 3.1416 rad = 180°

Interpretace jednotkového kruhu

Na jednotkovém kruhu (poloměr 1) je x přilehlou stranou pravého trojúhelníku postaveného od kladné osy x k bodu na kruhu a √(1 − x²) je protilehlou stranou. Arccos vrací úhel θ, který umisťuje bod na (x, √(1 − x²)) na horní polokouli nebo (x, 0) na koncích. Plátno zobrazuje poloměr k tomuto bodu a přerušované projekce na osy.

Obvyklé použití arccos

• Úhel mezi vektory: s normalizovanými vektory u a v, u·v = cos(θ) ⇒ θ = arccos(u·v).
• Geometrie a trojúhelníky: získání úhlu z délek stran pomocí Kosinové věty.
• Robotika a 3D grafika: převod skalárních součinů na úhly pro osvětlení, kameru a výpočty pozic.
• Zpracování signálů: fázové vztahy a korelační úhly.

Poznámky k přesnosti a zaokrouhlení

• Vstup s plovoucí desetinnou čárkou blízko ±1 může zesílit zaokrouhlovací šum. Pokud se objeví hodnota jako 1.0000001, omezte ji na 1 pro stabilní výsledek.
• Radiány mají přesné jednoduché formy pro speciální úhly (π/3, π/2, π). Desetinný displej zobrazí zaokroulené aproximace.
• Pokud potřebujete maximální přesnost, zvyšte ovládání desetinných míst a přečtěte si hodnotu v radiánech.

Často kladené otázky

Je arccos totéž jako cos⁻¹?
Ano. cos⁻¹(x) znamená inverzní funkci arccos(x), nikoli 1/cos(x).

Proč kalkulátor odmítá hodnoty menší než −1 nebo větší než 1?
Pro reálné úhly je kosinus omezen na [−1, 1]. Vstupy mimo tento interval nemají reálný arccos.

Proč dostávám pouze jeden úhel?
Kalkulátor vrací hlavní hodnotu v [0, π]. Existují další kotangenciální nebo doplňkové úhly, ale hlavní větev je standardní pro inverzní trigonometrické funkce a udržuje výsledky předvídatelné.

Mám používat stupně nebo radiány?
Používejte stupně pro každodenní interpretaci a radiány pro kalkulus, fyziku a většinu programovacích knihoven.

Jaký je váš případ použití tohoto kalkulátoru? Chtěli byste další nástroje nebo funkce? Dejte nám vědět v komentářích!

CalcuLife.com