Arc Length Online Calculator computes the length of a circular arc, the chord spanning the arc, and the sector area from radius and central angle. It has a nice visualization of each one. Formulas follow standard plane-geometry definitions.
How to use
- Enter the radius.
- Enter the central angle and choose deg or rad.
- Pick decimal places for rounding.
- Click Calculate. Results show below and the graphic highlights the sector.
Inputs and options
- Radius (r): non-negative real number.
- Angle (θ): use degrees or radians. Full circle is 360° = 2π rad.
- Units: cm, m, mm, in, ft. Outputs match the chosen length unit.
- Decimal places: 0–8. Controls rounding of all outputs and the labels on the diagram.
Formulas
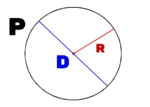
Let r be radius and θ the central angle in radians.
- Arc length (s): s = r·θ.
- Chord length (c): c = 2r·sin(θ/2).
- Sector area (A): A = ½·r²·θ.
When the angle is given in degrees (α), the calculator converts with θ = α·π/180. See also the sector identities in Wikipedia: Circular sector.
Units and conversions
- Arc and chord are lengths, reported in the selected unit (cm, m, mm, in, ft).
- Sector area reports in the corresponding squared unit (cm², m², mm², in², ft²).
- Changing the unit only changes labeling; it does not rescale your input. Enter r in the same unit you select.
Valid ranges and notes
- θ may be any real number. The visualization displays θ modulo 2π; outputs use the signed θ you entered.
- r = 0 gives s = 0, c = 0, A = 0.
- Negative r is not defined for a circle; the tool rejects it.
Quick examples
- Example 1: r = 10 cm, θ = 60° → θ = π/3 rad. s = 10·π/3 ≈ 10.472 cm; c = 2·10·sin(π/6) = 10 cm; A = ½·100·π/3 ≈ 52.360 cm².
- Example 2: r = 2 m, θ = 2 rad → s = 4 m; c = 2·2·sin(1) ≈ 3.365 m; A = ½·4·2 = 4 m².
Accuracy and rounding
- Internal math uses IEEE-754 double precision.
- Display rounding is controlled by your decimal-places setting; computation is not truncated.
FAQ
Arc vs chord? Arc length follows the circle; chord is the straight line between the endpoints.
Why radians? The natural form of the arc relation s = r·θ uses radians. Degrees are converted internally.
Full circumference? Set θ = 2π rad (or 360°). The arc equals the circle’s circumference 2πr. Reference: MathWorld: Circle.






Leave A Comment