Ball Volume Online Calculator

The ball is one of the fundamental geometric shapes. In real life, balls of perfect shape are not found very often, but at school or university you may encounter the task of calculating the volume of the ball. Either you need to make balls for the bearing or calculate the volume of basketballs. We suggest you use our simple and quick ball volume calculator. You can also convert the result to the desired measure of volume.

Share this?

Use this online calculator to compute the volume of a sphere from either radius or diameter. Results appear in cm³, m³, in³, and ft³. Supported length units: centimetres (cm), metres (m), inches (in), feet (ft). Supported volume units: cubic centimetres (cm³), cubic metres (m³), cubic inches (in³), cubic feet (ft³).

How to use

Choose Measurement Type (radius or diameter).
Enter the numeric value and select its Unit (cm, m, in, ft).
Click Calculate. The canvas labels the chosen dimension; the results panel shows volume in all units plus radius, diameter, circumference, and surface area.
Use Copy Results to copy the summary text. The button enables after a valid calculation.

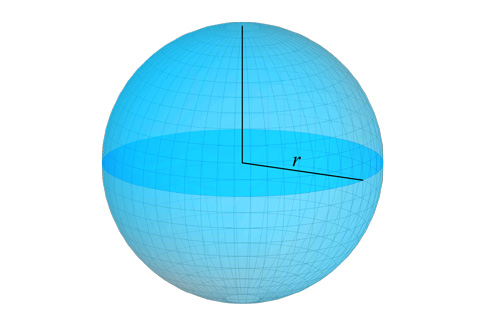
The radius of a ball is the distance from its center to its edge

Definitions of units

Centimetre (cm) — SI length unit. 1 m = 100 cm. Exact relation to inch: 1 in = 2.54 cm (exact).
Metre (m) — SI base length unit. 1 m = 39.3700787402 in (derived from 1 in = 2.54 cm exact) and 1 m = 3.280839895 ft. For volume, 1 m³ = 1,000,000 cm³ and 1 m³ = 1,000 L.
Inch (in) — US customary/imperial length unit. Defined exactly as 1 in = 2.54 cm. 12 in = 1 ft.
Foot (ft) — US customary/imperial length unit. 1 ft = 12 in = 0.3048 m (exact). 1 ft³ = 1728 in³.
Cubic centimetre (cm³) — SI-derived volume unit. 1 cm³ = 1 mL. Exact relation: 1 in³ = 16.387064 cm³.
Cubic metre (m³) — SI base volume unit. 1 m³ = 35.3146667 ft³ = 61,023.7441 in³ (exact factors).
Cubic inch (in³) — US customary/imperial volume unit. Exact relation: 1 in³ = 16.387064 cm³.
Cubic foot (ft³) — US customary/imperial volume unit. 1 ft³ = 1728 in³ = 0.028316846592 m³ (exact).

Formula

Sphere volume uses the formula V = (4/3)·π·r³. If diameter d is given, r = d/2; circumference on a great circle is C = 2·π·r; surface area is A = 4·π·r². Reference: Wolfram MathWorld — Sphere.

Reference table (radius in cm → volume)

Radius (cm)	Volume (cm³)	Volume (m³)	Volume (in³)
0.50	0.524	0.000001	0.032
1.00	4.189	0.000004	0.256
1.50	14.137	0.000014	0.863
2.00	33.510	0.000034	2.045
2.50	65.450	0.000065	3.994
3.00	113.097	0.000113	6.902
4.00	268.083	0.000268	16.359
5.00	523.599	0.000524	31.952
6.00	904.779	0.000905	55.213
7.50	1767.146	0.001767	107.838
10.00	4188.790	0.004189	255.616
12.50	8181.231	0.008181	499.249
15.00	14137.167	0.014137	862.703
20.00	33510.322	0.033510	2044.925
25.00	65449.847	0.065450	3993.995
30.00	113097.336	0.113097	6901.623
35.00	179594.380	0.179594	10959.521
40.00	268082.573	0.268083	16359.402
50.00	523598.776	0.523599	31951.958
60.00	904778.684	0.904779	55212.983

Real-world examples of balls volume

Table tennis ball, diameter 40.0 mm — Volume 33.510 cm³ and 2.045 in³.
Croquet ball, diameter 92.0 mm — Volume 407.720 cm³ and 24.881 in³.
Gumball, diameter 1.000 in (standard vending size) — Volume 8.580 cm³ and 0.524 in³.
Spherical ice ball, diameter 2.50 in (common bar mold) — Volume 134.066 cm³ and 8.181 in³.
Christmas ornament sphere, diameter 80.0 mm (common retail nominal) — Volume 268.083 cm³ and 16.359 in³.
Marble, diameter 1/2 in (peewee size) — Volume 1.073 cm³ and 0.065 in³.
Marble, diameter 16.0 mm (5/8-in class) — Volume 2.145 cm³ and 0.131 in³.
Spherical candle, diameter 3.00 in — Volume 231.667 cm³ and 14.137 in³.
Pool ball, diameter 57.15 mm — Volume 97.734 cm³ and 5.964 in³.
Snooker ball, diameter 52.5 mm — Volume 75.766 cm³ and 4.624 in³.