Cosinus Online Lommeregner – Enkel og Præcis Værktøj

Vores Cosinusberegner er et enkelt online værktøj, der beregner cosinus for en given vinkel i grader. Den er designet til alle, der har brug for hurtige og præcise trigonometriske beregninger, især nyttig for studerende, lærere og fagfolk inden for matematik og fysik.

Del dette?

Kopiér link ✓

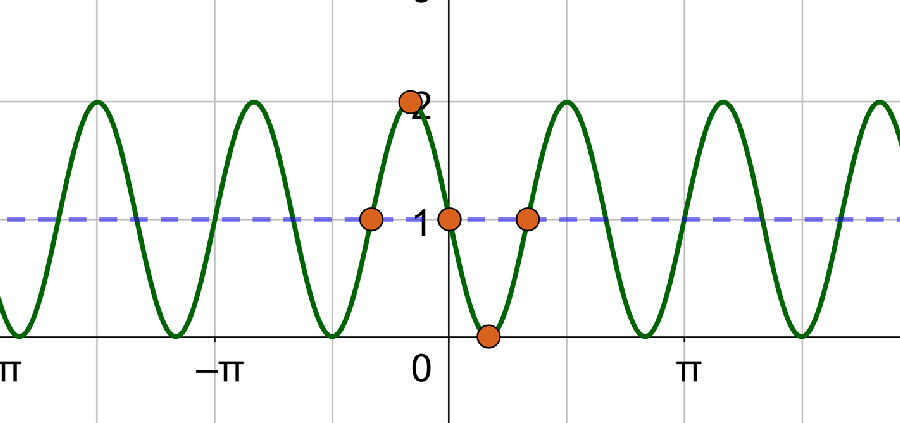
Graf over cosinus

Sådan bruger du beregneren

Det er nemt og intuitivt at bruge beregneren:

1. Indtast den ønskede vinkel i grader i inputfeltet. Der er ingen begrænsning på værdierne, du kan indtaste.
2. Klik på ‘Beregn Cosinus’ for at få cosinusværdien af den indtastede vinkel.
3. Resultatet vises straks, og viser cosinus af vinklen.
4. Hvis du har brug for at udføre en anden beregning, skal du blot klikke på ‘Ryd’ for at nulstille input og output.

Forståelse af Cosinusfunktionen

Cosinus er en grundlæggende trigonometrisk funktion, der relaterer en vinkel i en retvinklet trekant til forholdet mellem den tilstødende side og hypotenusen. Formlen for cosinus er:

• cosinus(θ) = tilstødende / hypotenuse

Her er θ vinklen i grader. Beregneren konverterer internt denne vinkel til radianer, da cosinusfunktionen i de fleste programmeringssprog, herunder JavaScript, bruger radianer til trigonometriske beregninger.

Uddannelsesmæssige indsigter om Cosinus

Cosinusfunktionen er afgørende for at forstå cirkulær bevægelse, bølgemønstre og svingninger i fysik. Den er vigtig for at beregne projektioner, bestemme kraftkomponenter i mekanik og i forskellige ingeniørapplikationer.

I felter som arkitektur og landmåling bruges cosinus til at bestemme afstande og vinkler. Den er også vital i computer grafik til at gengive 3D-modeller og beregne synsvinkler.

En grundig forståelse af cosinusfunktionen er essentiel for alle, der studerer eller arbejder inden for videnskabelige felter, hvor vinkler og deres relationer er centrale. Vores Cosinusberegner forenkler disse beregninger og hjælper med en dybere forståelse og praktisk anvendelse af disse koncepter.