在線 Arccos 計算器 – 反餘弦函數

使用此反餘弦（arccos）計算器來從餘弦值 x 獲得主角度 θ。該工具背後的數學遵循 NIST 數學函數數位圖書館所記錄的反圓形函數的標準定義（請參見 dlmf.nist.gov/4.23）。

要分享这个吗？

复制链接 ✓

反餘弦計算器的運作方式

1. 您輸入一個介於 −1 和 1 之間的數字 x。
2. 該工具計算 θ = arccos(x) 作為主值（以弧度表示），然後也顯示度數。
3. 它還顯示 sin(θ) 以及半徑、投影和點的清晰單位圓視覺化。

定義和公式

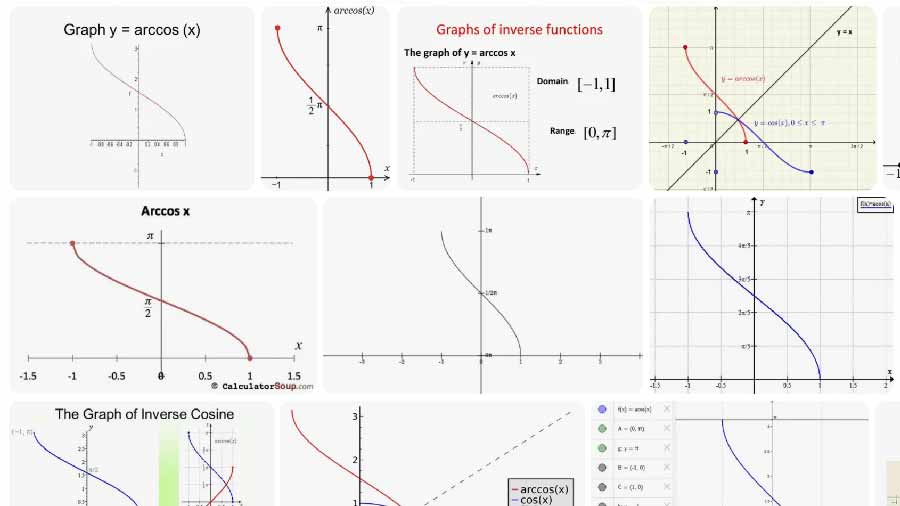
反餘弦返回滿足 cos(θ) = x 的主角度 θ。

• 輸入範圍：x ∈ [−1, 1]
• 輸出範圍（主值）：θ ∈ [0, π] 弧度，即 [0°, 180°]
• 轉換：度數 = 弧度 × 180/π

關鍵恆等式：如果 cos(θ) = x，則 θ = arccos(x)。對於主範圍以外的角度，還存在其他解：2π − θ 等等。此工具設計上報告主值。

輸入、輸出和精度

• 有效輸入 x：任何介於 −1 和 1 之間的實數。超出此範圍的值對於實角度是未定義的。
• 角度格式：該工具同時顯示度數和弧度。
• 小數位數：使用“十進位數”控制來設置四捨五入（0–10）。弧度通常需要 4–6 位小數；度數通常 2–4 位小數即可。

快速範例

• x = 1 → θ = 0 rad = 0°
• x = 0.5 → θ = arccos(0.5) = π/3 ≈ 1.0472 rad ≈ 60°
• x = 0 → θ = π/2 ≈ 1.5708 rad ≈ 90°
• x = −1 → θ = π ≈ 3.1416 rad = 180°

單位圓解釋

在單位圓（半徑為 1）上，x 是從正 x 軸到圓上點所構建的直角三角形的鄰邊，而 √(1 − x²) 是對邊。反餘弦返回的角度 θ 將該點放置在 (x, √(1 − x²)) 的上半圓或 (x, 0) 的端點。畫布顯示到該點的半徑以及虛線投影到坐標軸。

反餘弦的常見用途

• 向量之間的角度：對於標準化的向量 u 和 v，u·v = cos(θ) ⇒ θ = arccos(u·v)。
• 幾何和三角形：通過餘弦定理從邊長恢復角度。
• 機器人技術和 3D 圖形：將點積轉換為光照、相機和姿勢計算的角度。
• 信號處理：相位關係和相關角度。

準確性和四捨五入注意事項

• 接近 ±1 的浮點輸入可能會放大四捨五入噪聲。如果出現像 1.0000001 的值，請將其限制為 1 以獲得穩定的結果。
• 弧度對於特殊角度（π/3、π/2、π）具有精確的簡單形式。小數顯示將顯示四捨五入的近似值。
• 如果您需要最大精度，請增加小數位控制並讀取弧度值。

常見問題

反餘弦是否等於 cos⁻¹？
是的。cos⁻¹(x) 意味著反函數 arccos(x)，而不是 1/cos(x)。

為什麼計算器拒絕小於 −1 或大於 1 的值？
對於實角度，餘弦的範圍限制在 [−1, 1]。超出該區間的輸入沒有實數反餘弦。

為什麼我只得到一個角度？
計算器返回主值在 [0, π] 之內。還存在其他同角或補角，但主分支是反三角函數的標準，保持結果可預測。

我應該使用度數還是弧度？
日常解釋使用度數，計算、物理和大多數編程庫則使用弧度。

您使用此計算器的情況是什麼？您希望有其他工具或功能嗎？請在評論中告訴我們！

CalcuLife.com