Calcolatore Arccos Online – Coseno Inverso

Utilizza questo calcolatore di Arccos (coseno inverso) per ottenere l’angolo principale θ da un valore di coseno x. La matematica dietro lo strumento segue la definizione standard delle funzioni circolari inverse come documentato dalla Digital Library of Mathematical Functions del NIST (vedi Funzioni Circolari Inverse su dlmf.nist.gov/4.23).

Condividere questo?

Copia link ✓

Come funziona il calcolatore di arccos

1. Inserisci un numero x compreso tra −1 e 1.
2. Lo strumento calcola θ = arccos(x) come valore principale in radianti, quindi mostra anche i gradi.
3. Visualizza anche sin(θ) e una chiara visualizzazione del cerchio unitario con il raggio, le proiezioni e il punto.

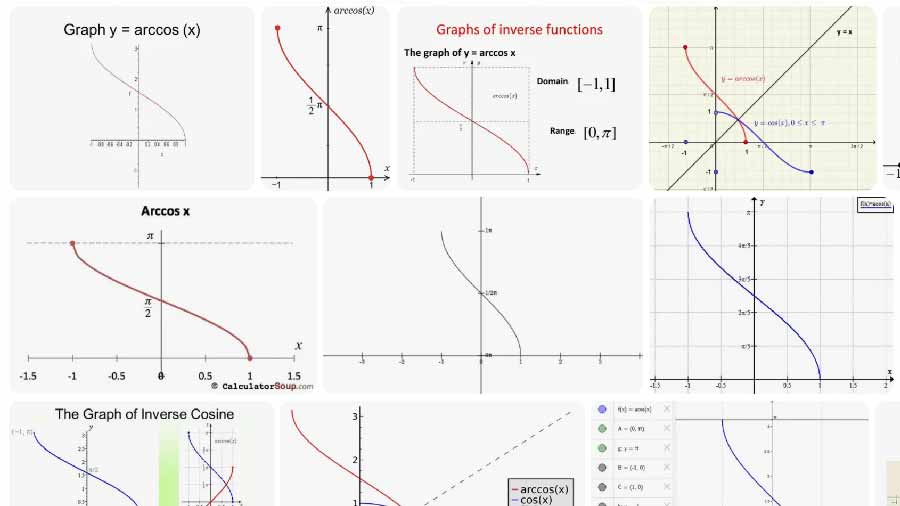
Definizione e formula

Arccos restituisce l’angolo principale θ che soddisfa cos(θ) = x.

• Dominio di input: x ∈ [−1, 1]
• Intervallo di output (valore principale): θ ∈ [0, π] radianti, che corrisponde a [0°, 180°]
• Conversione: gradi = radianti × 180/π

Identità chiave: se cos(θ) = x, allora θ = arccos(x). Per angoli al di fuori dell’intervallo principale, esistono altre soluzioni: 2π − θ, ecc. Questo strumento riporta il valore principale per design.

Input, output e precisione

• Input valido x: qualsiasi numero reale da −1 a 1. I valori al di fuori di questo intervallo non sono definiti per angoli reali.
• Formati angolari: lo strumento mostra sia i gradi che i radianti.
• Decimali: utilizza il controllo “Decimali” per impostare l’arrotondamento (0–10). I radianti spesso beneficiano di 4–6 decimali; i gradi sono comunemente adeguati con 2–4.

Esempi rapidi

• x = 1 → θ = 0 rad = 0°
• x = 0.5 → θ = arccos(0.5) = π/3 ≈ 1.0472 rad ≈ 60°
• x = 0 → θ = π/2 ≈ 1.5708 rad ≈ 90°
• x = −1 → θ = π ≈ 3.1416 rad = 180°

Interpretazione del cerchio unitario

Nel cerchio unitario (raggio 1), x è il lato adiacente del triangolo rettangolo costruito dall’asse x positivo al punto sul cerchio, e √(1 − x²) è il lato opposto. Arccos restituisce l’angolo θ che posiziona il punto a (x, √(1 − x²)) sulla semicirconferenza superiore o (x, 0) agli estremi. La tela mostra il raggio fino a quel punto e proiezioni tratteggiate sugli assi.

Usi comuni di arccos

• Angolo tra vettori: con vettori normalizzati u e v, u·v = cos(θ) ⇒ θ = arccos(u·v).
• Geometria e triangoli: recupera un angolo dalle lunghezze dei lati tramite la Legge dei Coseni.
• Robotica e grafica 3D: converti prodotti scalari in angoli per illuminazione, telecamera e calcoli di posa.
• Elaborazione dei segnali: relazioni di fase e angoli di correlazione.

Note su accuratezza e arrotondamento

• Input in virgola mobile vicino a ±1 può amplificare il rumore di arrotondamento. Se appare un valore come 1.0000001, limitalo a 1 per un risultato stabile.
• I radianti portano forme semplici esatte per angoli speciali (π/3, π/2, π). La visualizzazione decimale mostrerà approssimazioni arrotondate.
• Se hai bisogno di massima precisione, aumenta il controllo dei decimali e leggi il valore in radianti.

FAQ

Arccos è lo stesso di cos⁻¹?
Sì. cos⁻¹(x) significa la funzione inversa arccos(x), non 1/cos(x).

Perché il calcolatore rifiuta valori inferiori a −1 o superiori a 1?
Per angoli reali, il coseno è limitato a [−1, 1]. Gli input al di fuori di quell’intervallo non hanno un arccos reale.

Perché ottengo solo un angolo?
Il calcolatore restituisce il valore principale in [0, π]. Esistono altri angoli co-terminali o supplementari, ma il ramo principale è standard per le funzioni trigonometriche inverse e mantiene i risultati prevedibili.

Dovrei usare gradi o radianti?
Usa i gradi per l’interpretazione quotidiana e i radianti per calcolo, fisica e la maggior parte delle librerie di programmazione.

Qual è il tuo caso d’uso di questo calcolatore? Vorresti altri strumenti o funzionalità? Facci sapere nei commenti!

CalcuLife.com