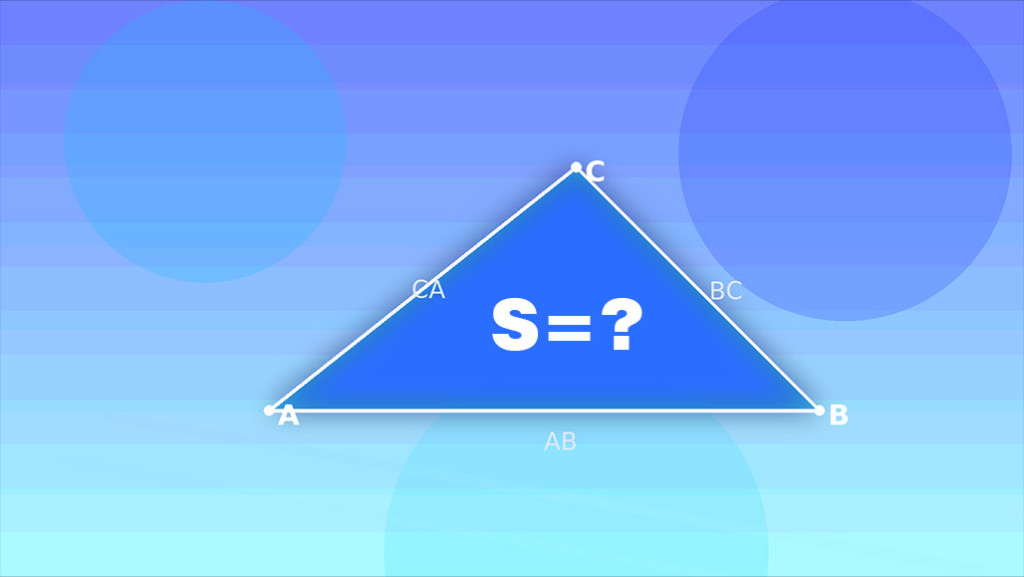
Calculatrice en ligne de l’aire d’un triangle à partir de trois côtés

Cette calculatrice en ligne calcule l’aire d’un triangle à partir de trois longueurs de côtés (AB, BC, CA) en utilisant la formule de Héron. Elle vérifie l’inégalité triangulaire, affiche un diagramme proportionnel avec les sommets A, B, C et trace une « tentative de toit » pour les ensembles impossibles. Le diagramme conserve les longueurs des côtés dans les bonnes proportions visuelles. Les étiquettes apparaissent sur les arêtes (AB, BC, CA) et sur les sommets (A, B, C).

Calculatrice d’aire de triangle (3 côtés)

Saisissez les longueurs des côtés AB, BC, CA. L’aire (S) est calculée avec la formule de Héron. Le schéma conserve les proportions et affiche A, B, C ainsi que AB, BC, CA. Si les côtés ne forment pas un triangle, un « toit » avec l’écart est tracé et le résultat indique « n’existe pas ».

Visualisation du triangle

Côté AB

Côté BC

Côté CA

Aire (S)

Le calcul s’affichera ici.

Décimales

Partager ceci ?

Mode d’emploi

Saisissez trois longueurs positives pour AB, BC et CA.
Cliquez sur Calculer.
Lisez l’aire S et consultez le calcul ainsi que le diagramme.
Utilisez Décimales pour contrôler l’arrondi du résultat et des étiquettes.

Remarques : Si les côtés ne peuvent pas former un triangle, le résultat affiche « n’existe pas » et la visualisation trace le plus grand côté comme base avec deux bras pointillés qui ne se rejoignent pas, soulignant l’écart.

Utilisez des unités cohérentes pour tous les côtés ; l’aire sera exprimée dans les unités carrées correspondantes (m², cm², in², ft², etc.).

Formules

Inégalité triangulaire (existence) : AB + BC > CA, AB + CA > BC, BC + CA > AB (toutes strictes).

Demi-périmètre : s = (AB + BC + CA) / 2

Formule de Héron (aire) : S = √[ s(s − AB)(s − BC)(s − CA) ]

Forme équivalente : S = (1/4) √[(AB + BC + CA)(−AB + BC + CA)(AB − BC + CA)(AB + BC − CA)].
De l’aire à la hauteur sur AB : h_AB = 2S / AB (de même pour les autres bases).
Avec le rayon inscrit r et le rayon circonscrit R : S = r·s = (AB·BC·CA)/(4R).
Équilatéral (côté a) : S = (√3/4)·a².

Exemples

AB	BC	CA	Valide ?	Aire S
3	4	5	Oui	6
5	5	6	Oui	12
7	5	6	Oui	14.6969
8	8	8	Oui	27.7128
10	6	8	Oui	24
9	12	15	Oui	54
2.5	4	5	Oui	4.9525
12	13	5	Oui	30
20	13	7	Non	—
6.5	6.5	4.2	Oui	12.918
15	14	9	Oui	61.6441
30	29	10	Oui	144.6373
100	120	150	Oui	5981.168
1.2	1.3	2.4	Oui	0.4196
9	9	18	Non	—

Faits intéressants

Résultat de Héron : La formule est attribuée à Héron d’Alexandrie (Ier siècle ap. J.-C.) et ne nécessite que les longueurs des côtés, sans angles ni hauteurs.
Triangles héroniens : Les triangles avec des côtés entiers et une aire entière (par ex. 3-4-5 avec S = 6) sont appelés héroniens.
Aire maximale : Pour un périmètre fixe, le triangle équilatéral a la plus grande aire. Pour deux côtés fixes, l’aire est maximale quand l’angle compris est de 90°.
Dégénérescence : Quand la somme de deux côtés est égale au troisième (par ex. 20, 13, 7), le « triangle » s’effondre en un segment et S = 0.
Vérifications : À partir de S et d’une base, on peut obtenir directement les hauteurs, le rayon inscrit (r = S/s) et le rayon circonscrit (R = AB·BC·CA/(4S)).

CalcuLife.com