Unser Tangens-Rechner ist ein praktisches Online-Tool, das entwickelt wurde, um den Tangens eines bestimmten Winkels in Grad zu berechnen. Es ist eine wertvolle Ressource für Schüler, Lehrer und Fachleute in Bereichen, die trigonometrische Berechnungen erfordern, wie Mathematik, Physik, Ingenieurwesen und Vermessung. Besonders in Deutschland, wo präzise Berechnungen in der Ingenieurwissenschaft und Architektur von großer Bedeutung sind, findet dieses Tool breite Anwendung.

Tangens Rechner

Kotangens
Das hier teilen?
WhatsApp X Telegram Facebook LinkedIn Reddit

 

Online Tangentenrechner mit Visualisierung

So verwenden Sie den Rechner

Der Rechner ist benutzerfreundlich:

  1. Geben Sie den Winkel in Grad ein, für den Sie den Tangens berechnen möchten, in das Eingabefeld ein.
  2. Klicken Sie auf ‘Tangens berechnen’, um das Ergebnis zu erhalten.
  3. Der Rechner zeigt den Tangens des Winkels an.
  4. Um eine neue Berechnung durchzuführen, klicken Sie einfach auf ‘Zurücksetzen’, um alles zurückzusetzen.

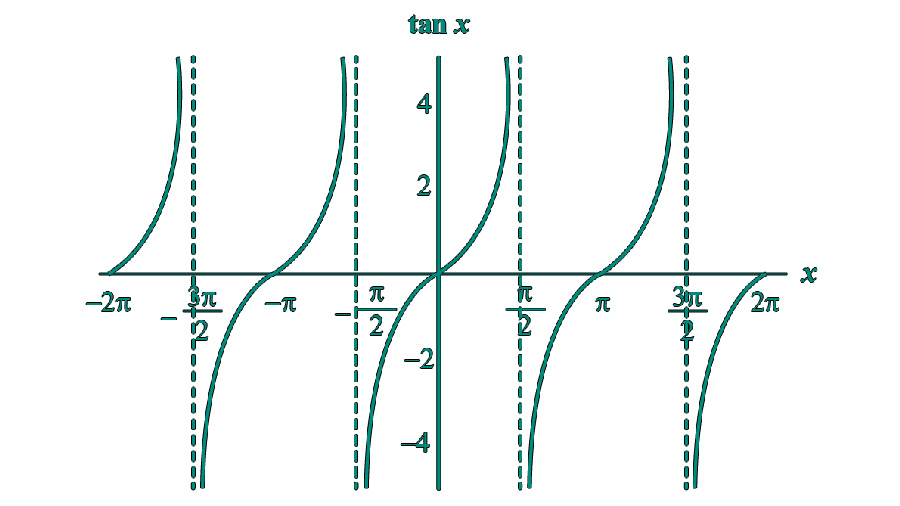
Verständnis der Tangensfunktion

Die Tangensfunktion ist eine der grundlegenden trigonometrischen Funktionen. Sie stellt einen Winkel in einem rechtwinkligen Dreieck in Beziehung zum Verhältnis der Länge der gegenüberliegenden Seite zur Länge der anliegenden Seite. Die Formel lautet:

  • tangens(θ) = gegenüberliegende Seite / anliegende Seite

Dabei ist θ der Winkel in Grad. Im Rechner wird der Winkel zunächst in Bogenmaß umgerechnet, da die Tangensfunktion in der Programmierung, einschließlich JavaScript, mit Bogenmaß arbeitet.

Bildungsinsights zum Tangens

Tangens spielt eine entscheidende Rolle in vielen wissenschaftlichen und ingenieurtechnischen Anwendungen. Er ist unerlässlich für das Verständnis von Wellenverhalten, Steigungen und Winkeln in der Geometrie. In der Physik wird der Tangens in Bewegungsproblemen verwendet und um Phänomene wie die Winkelgeschwindigkeit rotierender Objekte zu beschreiben.

In praktischen Anwendungen wird die Tangensfunktion in Bereichen wie Architektur zur Berechnung von Dachneigungen, in der Navigation zur Kursplanung und in der Vermessung zur Messung von Entfernungen eingesetzt. Das Verständnis der Tangensfunktion und ihrer Beziehung zu Winkeln kann die Problemlösungsfähigkeiten in verschiedenen technischen und wissenschaftlichen Bereichen erheblich verbessern.

© CalcuLife.com