O Calculador de Área de Trapézio encontra a área de um trapézio a partir de suas duas bases e altura usando a fórmula padrão da geometria. Os únicos dados que você precisa inserir são os comprimentos da base superior a, da base inferior b e da altura perpendicular h. A visualização centraliza e escala para os seus números, para que você possa ver qual lado é qual. Este tipo de ferramenta é especialmente útil no Brasil, onde o uso de trapézios é comum em projetos de arquitetura e engenharia.
Como o calculador funciona
- Entradas: Base superior a, base inferior b, altura h (todos números reais positivos).
- Fórmula:
Área = ((a + b) / 2) × h. Para uma referência concisa sobre a fórmula, veja Wolfram MathWorld: Trapézio. - Unidades: A saída é em unidades quadradas. Se as entradas estiverem em metros, o resultado será em m²; se em centímetros, em cm². A ferramenta deixa as unidades genéricas para se adequar a qualquer contexto.
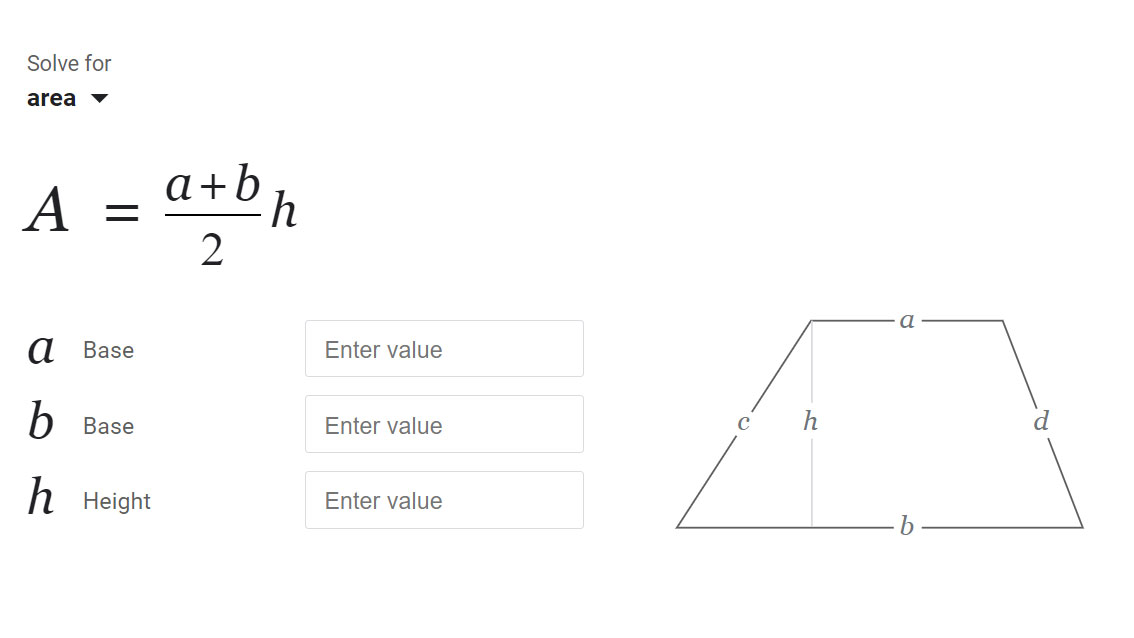
- Visualização: O diagrama permanece sempre centralizado na tela e rotula as mesmas quantidades que você digitou: a na parte superior, b na parte inferior e h como a distância perpendicular entre elas.
- Estabilidade numérica: A ferramenta aceita decimais, valores grandes e pequenos. Ela arredonda a exibição de forma limpa, mantendo a precisão interna.
Por que essa fórmula está correta
A área de um trapézio é igual à altura multiplicada pela média das duas bases paralelas. Intuitivamente, se você “deslizar” a base curta ao longo da altura, pode rearranjar o trapézio em um retângulo cuja largura é a média das duas bases. Isso resulta em A = h × (a + b)/2.
Exemplos passo a passo
- Exemplo 1 (corresponde ao desenho padrão):
- a = 6, b = 10, h = 4
- Média das bases = (6 + 10)/2 = 8
- Área = 8 × 4 = 32 unidades quadradas
- Exemplo 2 (decimais):
- a = 3,5, b = 12, h = 2,8
- Média das bases = (3,5 + 12)/2 = 7,75
- Área = 7,75 × 2,8 = 21,7 unidades quadradas
- Exemplo 3 (altura fina):
- a = 20, b = 24, h = 0,5
- Média das bases = 22
- Área = 22 × 0,5 = 11 unidades quadradas
Cálculos inversos que você pode precisar
- Resolver para a altura dada a área e as bases:
h = (2 × Área) / (a + b) - Resolver para uma base desconhecida dada a área, a outra base e a altura:
a = (2 × Área) / h − b(ou troque a e b)
O que conta como altura
A altura é perpendicular às bases. Não é o lado inclinado. Se os lados estão inclinados, a altura ainda é a menor distância reta entre as duas bases. Em trapézios retângulos ou isósceles, isso é fácil de ver; em casos obtusos, permanece perpendicular.
Verificações de qualidade e casos extremos
- Positividade: Todas as três entradas devem ser maiores que zero para produzir uma área.
- Bases iguais: Se a = b, o trapézio se torna um retângulo; a fórmula se reduz a
A = b × h, como esperado. - Números muito grandes ou muito pequenos: A área escala linearmente com a altura e com a média das bases. Dobrar cada entrada dobra a área para a altura e dobra para a média das bases, conforme apropriado.
Formas de trapézio no mundo real
- Seções transversais de estradas e medianas: Ombros e taludes frequentemente formam trapézios quando vistos de lado.
- Estruturas de telhados: Alguns painéis de telhados em hipérbole ou shed, e perfis de beiral, são trapezoidais.
- Jardins e rampas: Vistas de planta e perfis laterais frequentemente resultam em trapézios.
- Peças de chapa metálica e azulejos: Blank de trapézio são comuns na fabricação e em layouts de pisos.
- Valas e canais: Seções transversais de engenharia de valas frequentemente usam perfis trapezoidais.
Usando o resultado
- Estimativa de materiais: Multiplique a área pela espessura para aproximar o volume (por exemplo, solo ou concreto). Mantenha a consistência das unidades.
- Custos: Se um material é cobrado por unidade quadrada, multiplique o custo unitário pela sua área para estimar gastos.
- Escalonamento de desenhos: Se suas entradas vieram de um plano escalonado, converta para unidades do mundo real antes de calcular a área.
Erros comuns a evitar
- Usar um lado inclinado em vez da altura perpendicular.
- Adicionar unidades incorretamente. Mantenha todas as entradas na mesma unidade para que a saída esteja em quadrados dessa unidade.
- Esquecer que a fórmula usa a média das bases, não sua diferença.
CalcuLife.com






Deixar um comentário