Calculadora de Volume de Pirâmide Truncada

Este calculador online calcula o volume de um tronco de pirâmide (frustum) para bases quadradas e retangulares. Ele implementa a fórmula padrão de volume do tronco com manuseio consistente de unidades e controle de precisão. O método é baseado na geometria clássica (veja Frustum – Volume), portanto, os resultados são matematicamente confiáveis quando as entradas são válidas (dimensões não negativas com topo/base na mesma unidade). Este tipo de ferramenta é especialmente útil no Brasil, onde a construção civil frequentemente utiliza troncos de pirâmide em projetos arquitetônicos.

O que você irá inserir

Lado inferior a

Lado superior b

Altura h

Unidade

Decimais

Volume

—

Recapitulando Entradas

Fórmula

V = (h / 3) · (A_base + A_topo + √(A_base · A_topo))
Quadrado: A_base=a², A_topo=b² ⇒ V = (h/3)(a² + b² + ab)
Retangular: A_base=L₁·W₁, A_topo=L₂·W₂

A visualização utiliza uma projeção axonométrica fixa: os retângulos superior e inferior permanecem paralelos e centralizados; as arestas verticais escalam com sua altura. As guias marcam L (azul), W (verde) e h (vermelho).

Compartilhar isto?

Como Usar

Escolha o modo Quadrado, Retangular ou Áreas.
Insira:
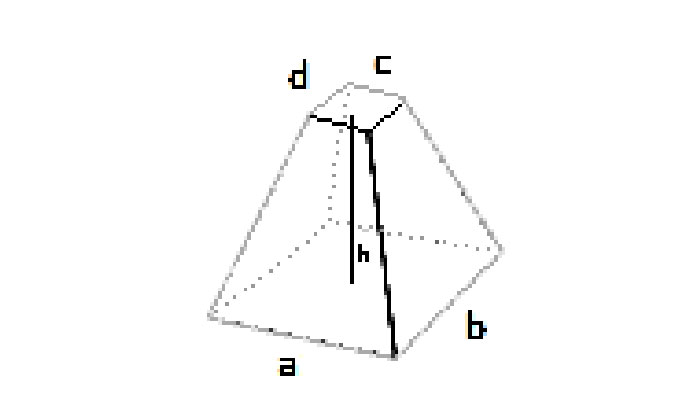
- Quadrado: lado inferior a, lado superior b, altura h.
- Retangular: base L₁ × W₁, topo L₂ × W₂, altura h.
- Áreas: área inferior A_bottom, área superior A_top, altura h.
Selecione a unidade e a precisão decimal, em seguida clique em Calcular.
A visualização reflete suas proporções: azul ≈ comprimento (L), verde ≈ largura (W), vermelho ≈ altura (h). A pílula abaixo mostra suas entradas para copiar/colar.

Fórmulas

Volume geral do tronco

V = (h / 3) · (A_bottom + A_top + √(A_bottom · A_top))

Bases quadradas (lado inferior a, lado superior b):
A_bottom = a², A_top = b² ⇒ V = (h / 3) · (a² + b² + a·b)

Bases retangulares (base L₁×W₁, topo L₂×W₂):
A_bottom = L₁·W₁, A_top = L₂·W₂ ⇒ V = (h / 3) · (L₁W₁ + L₂W₂ + √(L₁W₁·L₂W₂))

Verificações de sanidade. Se o topo for igual à base (A_top = A_bottom), a forma se torna um prisma e V = A_bottom·h. Se o topo for 0, é uma pirâmide completa e V = (A_bottom·h)/3.

Exemplos Pré-calculados (todas as entradas em cm; volumes em cm³)

Modo	Dimensões inferiores	Dimensões superiores	h	Volume
Quadrado	a × a = 10 × 10	b × b = 6 × 6	12	784
Quadrado	a × a = 5 × 5	b × b = 5 × 5	8	200
Quadrado	a × a = 20 × 20	b × b = 10 × 10	15	3.500
Quadrado	a × a = 7.5 × 7.5	b × b = 3.2 × 3.2	18	542,94
Retangular	L₁×W₁ = 12 × 8	L₂×W₂ = 6 × 4	20	1.120
Retangular	L₁×W₁ = 50 × 40	L₂×W₂ = 30 × 20	35	43.113,5263
Retangular	L₁×W₁ = 15 × 10	L₂×W₂ = 15 × 5	12	1.324,2641

Todos os valores verificados com V = (h/3)(A_bottom + A_top + √(A_bottomA_top)). Arredondamento mostrado para 2–4 casas decimais onde útil.

Dicas Práticas & Verificações de Qualidade

Mantenha as unidades consistentes. Insira todas as dimensões lineares na mesma unidade; o calculador converte para volume nessa unidade³ (por exemplo, cm → cm³).
Meça a altura corretamente. Use a distância perpendicular entre as bases (não uma aresta inclinada).
Use o modo Áreas quando você já souber as áreas das bases (a partir de desenhos, CAD ou medições de campo) para evitar erros de arredondamento acumulados.
Verificação de sanidade com extremos: Se b → a, o resultado deve se aproximar de A·h. Se b → 0, o resultado deve se aproximar de (A·h)/3.
Controle de precisão: Aumente “Decimais” quando as entradas forem pequenas ou quando você planeja encadear cálculos (por exemplo, para massa usando densidade).

CalcuLife.com