Arccos-kalkulator på nett – Invers cosinus

Bruk denne Arccos (invers kosinus) kalkulatoren for å få den primære vinkelen θ fra en kosinusverdi x. Matematikk bak verktøyet følger den standard definisjonen av de inverse sirkulære funksjonene som dokumentert av NISTs Digitale Bibliotek for Matematiske Funksjoner (se Inverse Sirkulære Funksjoner på dlmf.nist.gov/4.23).

Dele dette?

Kopier lenke ✓

Hvordan arccos kalkulatoren fungerer

1. Du skriver inn et tall x mellom −1 og 1.
2. Verktøyet beregner θ = arccos(x) som den primære verdien i radianer, og viser også grader.
3. Det viser også sin(θ) og en ren enhets-sirkel visualisering av radius, projeksjoner og punkt.

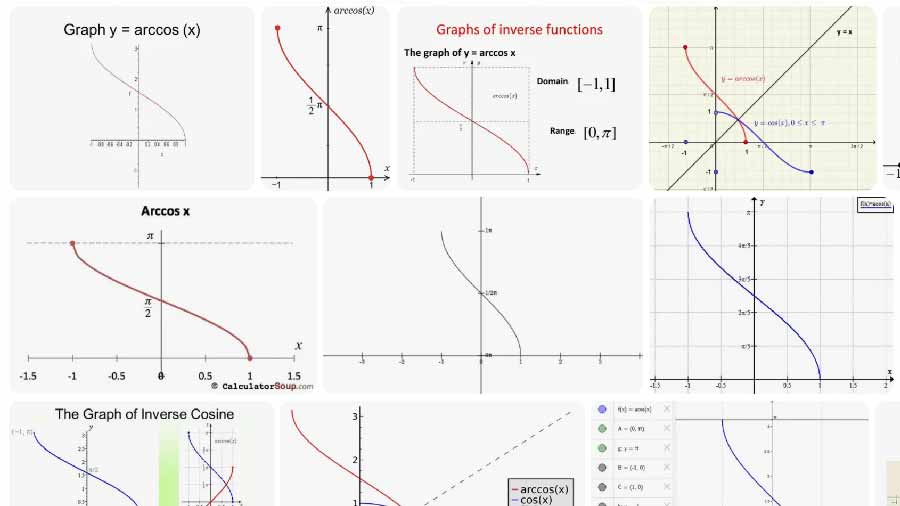
Definisjon og formel

Arccos returnerer den primære vinkelen θ som tilfredsstiller cos(θ) = x.

• Inndataområde: x ∈ [−1, 1]
• Utdatabredde (primærverdi): θ ∈ [0, π] radianer, som er [0°, 180°]
• Konvertering: grader = radianer × 180/π

Nøkkelidentitet: hvis cos(θ) = x, så θ = arccos(x). For vinkler utenfor den primære rekkevidden finnes det andre løsninger: 2π − θ, osv. Dette verktøyet rapporterer den primære verdien etter design.

Inndata, utdata og presisjon

• Gyldig inndata x: ethvert reelt tall fra −1 til 1. Verdier utenfor dette området er ikke definert for reelle vinkler.
• Vinkelformater: verktøyet viser både grader og radianer.
• Desimaler: bruk kontrollen for “Desimaler” for å sette avrunding (0–10). Radianer drar ofte nytte av 4–6 desimaler; grader er vanligvis fine med 2–4.

Raske eksempler

• x = 1 → θ = 0 rad = 0°
• x = 0.5 → θ = arccos(0.5) = π/3 ≈ 1.0472 rad ≈ 60°
• x = 0 → θ = π/2 ≈ 1.5708 rad ≈ 90°
• x = −1 → θ = π ≈ 3.1416 rad = 180°

Enhets-sirkel tolkning

På enhets-sirkelen (radius 1), er x den tilstøtende siden av den rette trekanten bygget fra den positive x-aksen til punktet på sirkelen, og √(1 − x²) er den motsatte siden. Arccos returnerer vinkelen θ som plasserer punktet ved (x, √(1 − x²)) på den øvre halvsirkelen eller (x, 0) ved endepunktene. Lerretet viser radius til det punktet og stiplete projeksjoner på aksene.

Vanlige bruksområder for arccos

• Vinkel mellom vektorer: med normaliserte vektorer u og v, u·v = cos(θ) ⇒ θ = arccos(u·v).
• Geometri og trekanter: gjenopprett en vinkel fra sidelengder via Cosinussetningen.
• Robotikk og 3D-grafikk: konverter dot-produkter til vinkler for belysning, kamera og posisjonsberegninger.
• Signalbehandling: faseforhold og korrelasjonsvinkler.

Nøyaktighet og avrundingsnotater

• Flyttallsinndata nær ±1 kan forsterke avrundingsstøy. Hvis en verdi som 1.0000001 vises, begrens den til 1 for et stabilt resultat.
• Radianer har eksakte enkle former for spesielle vinkler (π/3, π/2, π). Desimalvisningen vil vise avrundede tilnærminger.
• Hvis du trenger maksimal presisjon, øk kontrollen for desimaler og les radianverdien.

FAQ

Er arccos det samme som cos⁻¹?
Ja. cos⁻¹(x) betyr den inverse funksjonen arccos(x), ikke 1/cos(x).

Hvorfor avviser kalkulatoren verdier mindre enn −1 eller større enn 1?
For reelle vinkler er kosinus begrenset til [−1, 1]. Inndata utenfor dette intervallet har ingen reell arccos.

Hvorfor får jeg bare én vinkel?
Kalkulatoren returnerer den primære verdien i [0, π]. Andre coterminale eller supplementære vinkler finnes, men den primære grenen er standard for inverse trigonometriske funksjoner og holder resultatene forutsigbare.

Bør jeg bruke grader eller radianer?
Bruk grader for daglig tolkning og radianer for kalkulus, fysikk og de fleste programmeringsbiblioteker.

Hva er ditt tilfelle for å bruke denne kalkulatoren? Ønsker du noen andre verktøy eller funksjoner? Gi oss beskjed i kommentarene!

CalcuLife.com