アークコサイン計算機オンライン – 逆コサイン

このアークコサイン（逆コサイン）計算機を使用して、コサイン値 x から主角 θ を取得します。このツールの背後にある数学は、NISTのデジタル数学関数ライブラリに文書化されている逆円関数の標準定義に従っています（詳細は dlmf.nist.gov/4.23 を参照してください）。

これを共有しますか？

リンクをコピー ✓

アークコサイン計算機の仕組み

1. −1 と 1 の間の数 x を入力します。
2. ツールは θ = arccos(x) を主値としてラジアンで計算し、度数も表示します。
3. また、sin(θ) と半径、投影、点のクリーンな単位円のビジュアライゼーションも表示します。

定義と公式

アークコサインは、cos(θ) = x を満たす主角 θ を返します。

• 入力範囲: x ∈ [−1, 1]
• 出力範囲（主値）: θ ∈ [0, π] ラジアン、すなわち [0°, 180°]
• 変換: 度数 = ラジアン × 180/π

重要な恒等式: cos(θ) = x の場合、θ = arccos(x) です。主範囲外の角度には他の解が存在します: 2π − θ など。このツールは設計上、主値を報告します。

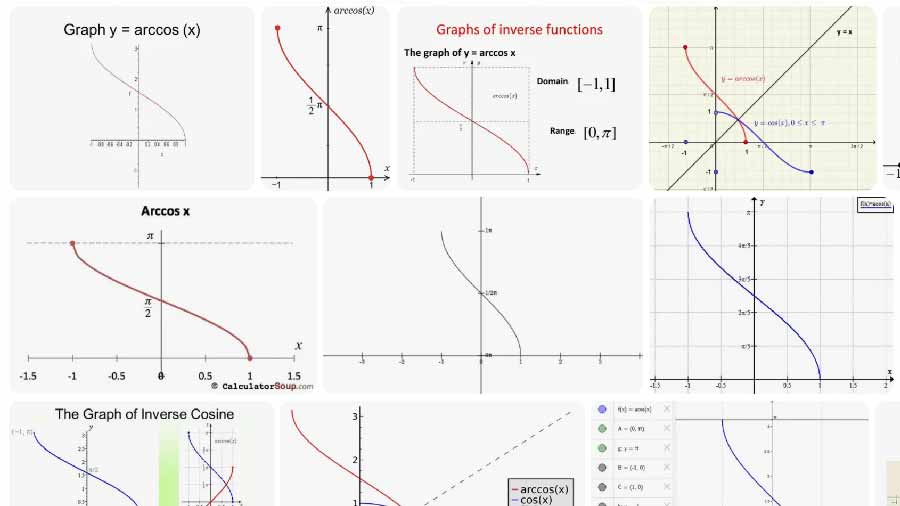
入力、出力、精度

• 有効な入力 x: −1 から 1 までの任意の実数。これらの範囲外の値は実角度に対して未定義です。
• 角度形式: ツールは度数とラジアンの両方を表示します。
• 小数点以下の桁数: “小数点以下の桁数”コントロールを使用して丸めを設定します（0–10）。ラジアンは通常4–6桁の小数が有利で、度数は一般的に2–4桁で十分です。

クイック例

• x = 1 → θ = 0 rad = 0°
• x = 0.5 → θ = arccos(0.5) = π/3 ≈ 1.0472 rad ≈ 60°
• x = 0 → θ = π/2 ≈ 1.5708 rad ≈ 90°
• x = −1 → θ = π ≈ 3.1416 rad = 180°

単位円の解釈

単位円（半径1）では、x は正の x 軸から円上の点までの直角三角形の隣接辺であり、√(1 − x²) は対辺です。アークコサインは、点 (x, √(1 − x²)) を上半円に配置する角度 θ を返します。また、端点では (x, 0) になります。キャンバスはその点までの半径と軸への破線の投影を示します。

アークコサインの一般的な使用法

• ベクトル間の角度: 正規化されたベクトル u と v に対して、u·v = cos(θ) ⇒ θ = arccos(u·v)。
• 幾何学と三角形: コサインの法則を用いて辺の長さから角度を求めます。
• ロボティクスと3Dグラフィックス: 照明、カメラ、ポーズ計算のためにドット積を角度に変換します。
• 信号処理: 位相関係と相関角度。

精度と丸めに関する注意

• ±1 に近い浮動小数点入力は、丸めノイズを増幅する可能性があります。1.0000001 のような値が表示された場合は、安定した結果のために1にクリンピングしてください。
• ラジアンは特別な角度（π/3、π/2、π）に対して正確な単純形を持ちます。小数表示は丸めた近似値を示します。
• 最大の精度が必要な場合は、小数点以下の桁数コントロールを増やし、ラジアン値を読み取ってください。

FAQ

アークコサインは cos⁻¹ と同じですか？
はい。cos⁻¹(x) は逆関数 arccos(x) を意味し、1/cos(x) ではありません。

なぜ計算機は −1 より小さい値や 1 より大きい値を拒否するのですか？
実角度に対して、コサインは [−1, 1] に制限されています。その区間外の入力には実際のアークコサインが存在しません。

なぜ一つの角度しか得られないのですか？
計算機は [0, π] の主値を返します。他の同角または補角が存在しますが、主分岐は逆三角関数の標準であり、結果を予測可能に保ちます。

度数とラジアンのどちらを使用すべきですか？
日常的な解釈には度数を、微積分、物理学、ほとんどのプログラミングライブラリにはラジアンを使用してください。

この計算機を使用するケースは何ですか？他に必要なツールや機能はありますか？コメントでお知らせください！

CalcuLife.com