Calculateur Arccos en ligne – Cosinus inverse

Utilisez ce calculateur d’Arccos (cosinus inverse) pour obtenir l’angle principal θ à partir d’une valeur de cosinus x. Les mathématiques derrière cet outil suivent la définition standard des fonctions circulaires inverses comme documenté par la Bibliothèque numérique des fonctions mathématiques du NIST (voir Fonctions circulaires inverses sur dlmf.nist.gov/4.23).

Partager ceci ?

Copier le lien ✓

Comment fonctionne le calculateur d’arccos

1. Vous entrez un nombre x compris entre −1 et 1.
2. L’outil calcule θ = arccos(x) comme la valeur principale en radians, puis affiche également les degrés.
3. Il affiche également sin(θ) et une visualisation claire du cercle unité avec le rayon, les projections et le point.

Définition et formule

Arccos renvoie l’angle principal θ qui satisfait cos(θ) = x.

• Domaine d’entrée : x ∈ [−1, 1]
• Plage de sortie (valeur principale) : θ ∈ [0, π] radians, ce qui correspond à [0°, 180°]
• Conversion : degrés = radians × 180/π

Identité clé : si cos(θ) = x, alors θ = arccos(x). Pour les angles en dehors de la plage principale, d’autres solutions existent : 2π − θ, etc. Cet outil rapporte la valeur principale par conception.

Entrées, sorties et précision

• Entrée valide x : tout nombre réel de −1 à 1. Les valeurs en dehors de cette plage sont indéfinies pour les angles réels.
• Formats d’angle : l’outil affiche à la fois les degrés et les radians.
• Chiffres décimaux : utilisez le contrôle « Chiffres décimaux » pour définir l’arrondi (0–10). Les radians bénéficient souvent de 4 à 6 décimales ; les degrés sont généralement bons avec 2 à 4.

Exemples rapides

• x = 1 → θ = 0 rad = 0°
• x = 0,5 → θ = arccos(0,5) = π/3 ≈ 1,0472 rad ≈ 60°
• x = 0 → θ = π/2 ≈ 1,5708 rad ≈ 90°
• x = −1 → θ = π ≈ 3,1416 rad = 180°

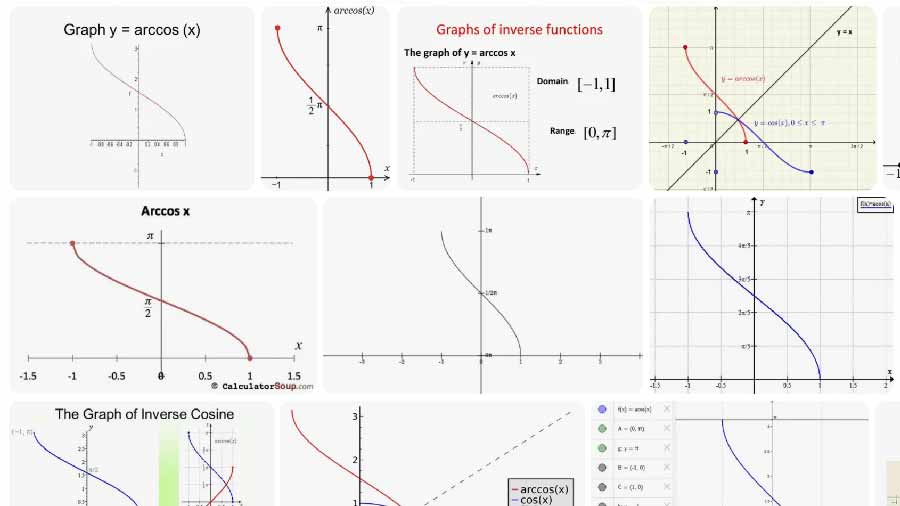
Interprétation du cercle unité

Sur le cercle unité (rayon 1), x est le côté adjacent du triangle rectangle construit à partir de l’axe x positif jusqu’au point sur le cercle, et √(1 − x²) est le côté opposé. Arccos renvoie l’angle θ qui place le point à (x, √(1 − x²)) sur le demi-cercle supérieur ou (x, 0) aux extrémités. Le canevas montre le rayon jusqu’à ce point et des projections en pointillés sur les axes.

Utilisations courantes de l’arccos

• Angle entre des vecteurs : avec des vecteurs normalisés u et v, u·v = cos(θ) ⇒ θ = arccos(u·v).
• Géométrie et triangles : récupérer un angle à partir des longueurs des côtés via la loi des cosinus.
• Robotique et graphismes 3D : convertir des produits scalaires en angles pour les calculs d’éclairage, de caméra et de pose.
• Traitement du signal : relations de phase et angles de corrélation.

Notes sur la précision et l’arrondi

• L’entrée en virgule flottante proche de ±1 peut amplifier le bruit d’arrondi. Si une valeur comme 1,0000001 apparaît, limitez-la à 1 pour un résultat stable.
• Les radians ont des formes simples exactes pour des angles spéciaux (π/3, π/2, π). L’affichage décimal montrera des approximations arrondies.
• Si vous avez besoin de la précision maximale, augmentez le contrôle des chiffres décimaux et lisez la valeur en radians.

FAQ

L’arccos est-il le même que cos⁻¹ ?
Oui. cos⁻¹(x) signifie la fonction inverse arccos(x), pas 1/cos(x).

Pourquoi le calculateur rejette-t-il les valeurs inférieures à −1 ou supérieures à 1 ?
Pour les angles réels, le cosinus est limité à [−1, 1]. Les entrées en dehors de cet intervalle n’ont pas d’arccos réel.

Pourquoi n’obtiens-je qu’un seul angle ?
Le calculateur renvoie la valeur principale dans [0, π]. D’autres angles coterminaux ou supplémentaires existent, mais la branche principale est standard pour les fonctions trigonométriques inverses et maintient les résultats prévisibles.

Dois-je utiliser des degrés ou des radians ?
Utilisez des degrés pour l’interprétation quotidienne et des radians pour le calcul, la physique et la plupart des bibliothèques de programmation.

Quel est votre cas d’utilisation de ce calculateur ? Souhaitez-vous d’autres outils ou fonctionnalités ? Faites-le nous savoir dans les commentaires !

CalcuLife.com