Der Trapezflächenrechner ermittelt die Fläche eines Trapezes anhand seiner beiden Basen und der Höhe unter Verwendung der standardmäßigen Geometrieformel. Die einzigen Eingaben, die Sie benötigen, sind die Längen der oberen Basis a, der unteren Basis b und der senkrechten Höhe h. Die Visualisierung zentriert sich und skaliert auf Ihre Zahlen, sodass Sie sehen können, welche Seite welche ist. Dieses Tool ist besonders nützlich für Schüler und Studenten in Deutschland, die Geometrie lernen und anwenden möchten.
Wie der Rechner funktioniert
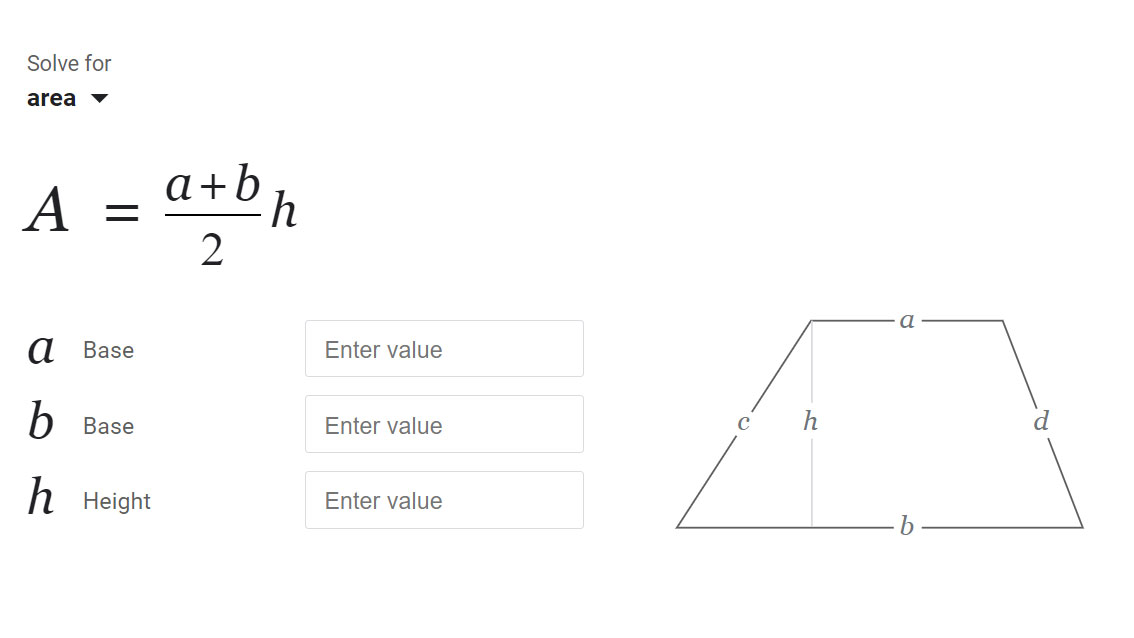
- Eingaben: Obere Basis a, untere Basis b, Höhe h (alle positiven reellen Zahlen).
- Formel:
Fläche = ((a + b) / 2) × h. Für eine prägnante Referenz zur Formel siehe Wolfram MathWorld: Trapez. - Einheiten: Die Ausgabe erfolgt in Quadrat-Einheiten. Wenn die Eingaben in Metern sind, ist das Ergebnis in m²; wenn in Zoll, in in². Das Tool lässt die Einheiten allgemein, um in jeden Kontext zu passen.
- Visualisierung: Das Diagramm bleibt immer zentriert auf der Leinwand und beschriftet die gleichen Größen, die Sie eingegeben haben: a oben, b unten und h als senkrechte Distanz zwischen ihnen.
- Numerische Stabilität: Das Tool akzeptiert Dezimalzahlen, große Werte und kleine Werte. Es rundet die Anzeige sauber, während die interne Präzision erhalten bleibt.
Warum diese Formel korrekt ist
Die Fläche eines Trapezes entspricht der Höhe multipliziert mit dem Durchschnitt der beiden parallelen Seiten. Intuitiv, wenn Sie die kurze Basis entlang der Höhe „verschieben“, können Sie das Trapez in ein Rechteck umformen, dessen Breite der Durchschnitt der beiden Basen ist. Das ergibt A = h × (a + b)/2.
Schritt-für-Schritt-Beispiele
- Beispiel 1 (entspricht der Standardzeichnung):
- a = 6, b = 10, h = 4
- Durchschnitt der Basen = (6 + 10)/2 = 8
- Fläche = 8 × 4 = 32 Quadrat-Einheiten
- Beispiel 2 (Dezimalzahlen):
- a = 3.5, b = 12, h = 2.8
- Durchschnitt der Basen = (3.5 + 12)/2 = 7.75
- Fläche = 7.75 × 2.8 = 21.7 Quadrat-Einheiten
- Beispiel 3 (schmale Höhe):
- a = 20, b = 24, h = 0.5
- Durchschnitt der Basen = 22
- Fläche = 22 × 0.5 = 11 Quadrat-Einheiten
Rückwärtsberechnungen, die Sie möglicherweise benötigen
- Höhe berechnen, gegeben Fläche und Basen:
h = (2 × Fläche) / (a + b) - Eine unbekannte Basis berechnen, gegeben Fläche, die andere Basis und Höhe:
a = (2 × Fläche) / h − b(oder a und b tauschen)
Was als Höhe zählt
Die Höhe ist senkrecht zu den Basen. Sie ist nicht die schräge Seite. Wenn die Seiten geneigt sind, ist die Höhe immer noch die kürzeste gerade Distanz zwischen den beiden Basen. Bei rechtwinkligen oder gleichschenkligen Trapezen ist dies leicht zu erkennen; in stumpfen Fällen bleibt sie senkrecht.
Qualitätsprüfungen und Randfälle
- Positivität: Alle drei Eingaben müssen größer als null sein, um eine Fläche zu erzeugen.
- Gleiche Basen: Wenn a = b, wird das Trapez zu einem Rechteck; die Formel reduziert sich auf
A = b × h, wie erwartet. - Sehr große oder sehr kleine Zahlen: Die Fläche skaliert linear mit der Höhe und mit dem Durchschnitt der Basen. Wenn jede Eingabe verdoppelt wird, verdoppelt sich die Fläche entsprechend für die Höhe und den Durchschnitt der Basen.
Trapezformen in der realen Welt
- Straßenquerschnitte und Mittelstreifen: Schultern und Böschungen bilden oft Trapeze, wenn sie von der Seite betrachtet werden.
- Dachkonstruktionen: Einige Hip- oder Satteldachpaneele und Gesimse sind trapezförmig.
- Landschaftsbau und Rampen: Grundrisse und Seitenprofile ergeben häufig Trapeze.
- Blechteile und Fliesen: Trapezbleche sind in der Fertigung und bei Bodenbelägen üblich.
- Gräben und Kanäle: Ingenieurquerschnitte von Gräben verwenden oft trapezförmige Profile.
Verwendung des Ergebnisses
- Materialschätzung: Multiplizieren Sie die Fläche mit der Dicke, um das Volumen abzuschätzen (z. B. Erde oder Beton). Achten Sie auf Einheitlichkeit der Einheiten.
- Kostenkalkulation: Wenn ein Material pro Quadrat-Einheit bepreist wird, multiplizieren Sie die Einheitspreise mit Ihrer Fläche, um die Ausgaben abzuschätzen.
- Zeichnungen skalieren: Wenn Ihre Eingaben aus einem maßstabsgetreuen Plan stammen, konvertieren Sie in reale Einheiten, bevor Sie die Fläche berechnen.
Häufige Fehler, die zu vermeiden sind
- Verwendung einer schrägen Seite anstelle der senkrechten Höhe.
- Einheiten falsch hinzufügen. Halten Sie alle Eingaben in derselben Einheit, damit die Ausgabe in Quadrat dieser Einheit erfolgt.
- Vergessen, dass die Formel den Durchschnitt der Basen verwendet, nicht deren Differenz.
CalcuLife.com








Hinterlasse einen Kommentar