Kalkulator Arccos Online – Cosinus Odwrotny

Użyj tego kalkulatora Arccos (funkcji odwrotnej cosinusa), aby uzyskać kąt główny θ z wartości cosinusa x. Matematyka stojąca za tym narzędziem opiera się na standardowej definicji odwrotnych funkcji trygonometrycznych, jak dokumentuje Biblioteka Cyfrowa Funkcji Matematycznych NIST (zobacz Funkcje Odwrotne na dlmf.nist.gov/4.23).

Udostępnić to?

Kopiuj link ✓

Jak działa kalkulator arccos

1. Wprowadzasz liczbę x między −1 a 1.
2. Narzędzie oblicza θ = arccos(x) jako wartość główną w radianach, a następnie pokazuje również w stopniach.
3. Wyświetla również sin(θ) oraz czystą wizualizację okręgu jednostkowego z promieniem, projekcjami i punktem.

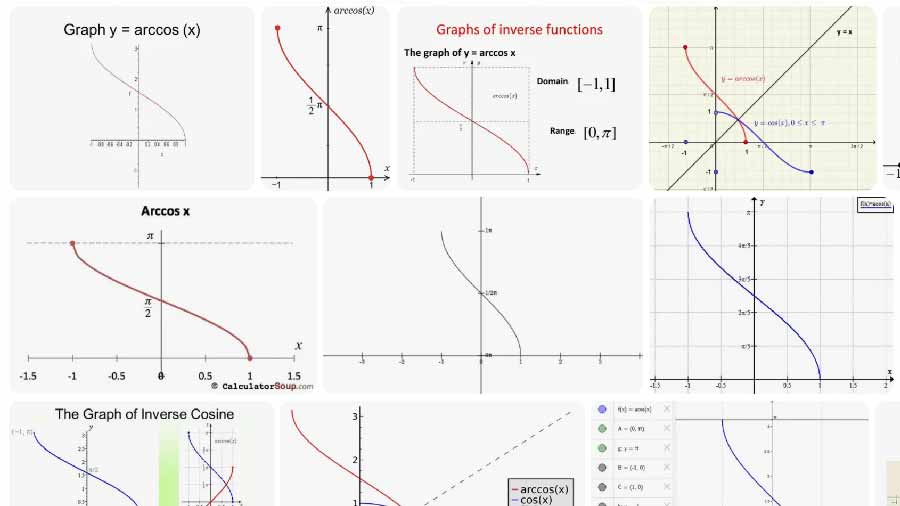
Definicja i wzór

Arccos zwraca kąt główny θ, który spełnia cos(θ) = x.

• Domena wejściowa: x ∈ [−1, 1]
• Zasięg wyjściowy (wartość główna): θ ∈ [0, π] radianów, co odpowiada [0°, 180°]
• Konwersja: stopnie = radiany × 180/π

Kluczowa tożsamość: jeśli cos(θ) = x, to θ = arccos(x). Dla kątów poza głównym zakresem istnieją inne rozwiązania: 2π − θ, itd. To narzędzie zgłasza wartość główną z założenia.

Wejścia, wyjścia i precyzja

• Poprawne wejście x: każda liczba rzeczywista od −1 do 1. Wartości poza tym zakresem są nieokreślone dla kątów rzeczywistych.
• Formaty kątów: narzędzie pokazuje zarówno stopnie, jak i radiany.
• Miejsca po przecinku: użyj kontrolki „Miejsca po przecinku”, aby ustawić zaokrąglenie (0–10). Radiany często korzystają z 4–6 miejsc po przecinku; stopnie zazwyczaj są w porządku z 2–4.

Szybkie przykłady

• x = 1 → θ = 0 rad = 0°
• x = 0.5 → θ = arccos(0.5) = π/3 ≈ 1.0472 rad ≈ 60°
• x = 0 → θ = π/2 ≈ 1.5708 rad ≈ 90°
• x = −1 → θ = π ≈ 3.1416 rad = 180°

Interpretacja okręgu jednostkowego

Na okręgu jednostkowym (promień 1), x jest przyprostokątną trójkąta prostokątnego zbudowanego od dodatniej osi x do punktu na okręgu, a √(1 − x²) jest drugą przyprostokątną. Arccos zwraca kąt θ, który umieszcza punkt w (x, √(1 − x²)) na górnej półokręgu lub (x, 0) na końcach. Płótno pokazuje promień do tego punktu oraz przerywane projekcje na osie.

Typowe zastosowania arccos

• Kąt między wektorami: dla znormalizowanych wektorów u i v, u·v = cos(θ) ⇒ θ = arccos(u·v).
• Geometria i trójkąty: odzyskiwanie kąta z długości boków za pomocą wzoru cosinusów.
• Robotyka i grafika 3D: konwersja iloczynów skalarnych na kąty do obliczeń oświetlenia, kamery i pozycji.
• Przetwarzanie sygnałów: relacje fazowe i kąty korelacji.

Uwagi dotyczące dokładności i zaokrąglania

• Wejście zmiennoprzecinkowe bliskie ±1 może potęgować szum zaokrągleń. Jeśli pojawi się wartość taka jak 1.0000001, ogranicz ją do 1 dla stabilnego wyniku.
• Radiany mają dokładne proste formy dla specjalnych kątów (π/3, π/2, π). Wyświetlanie dziesiętne pokaże zaokrąglone przybliżenia.
• Jeśli potrzebujesz maksymalnej precyzji, zwiększ kontrolkę miejsc po przecinku i odczytaj wartość w radianach.

FAQ

Czy arccos to to samo co cos⁻¹?
Tak. cos⁻¹(x) oznacza funkcję odwrotną arccos(x), a nie 1/cos(x).

Dlaczego kalkulator odrzuca wartości mniejsze niż −1 lub większe niż 1?
Dla kątów rzeczywistych cosinus jest ograniczony do [−1, 1]. Wejścia poza tym przedziałem nie mają rzeczywistego arccos.

Dlaczego otrzymuję tylko jeden kąt?
Kalkulator zwraca wartość główną w [0, π]. Istnieją inne kąty współrzędne lub dopełniające, ale główny zakres jest standardowy dla funkcji odwrotnych trygonometrycznych i utrzymuje wyniki przewidywalne.

Czy powinienem używać stopni czy radianów?
Używaj stopni do codziennej interpretacji, a radianów do rachunku różniczkowego, fizyki i większości bibliotek programistycznych.

Jakie jest Twoje zastosowanie tego kalkulatora? Czy chciałbyś inne narzędzia lub funkcje? Daj nam znać w komentarzach!

CalcuLife.com