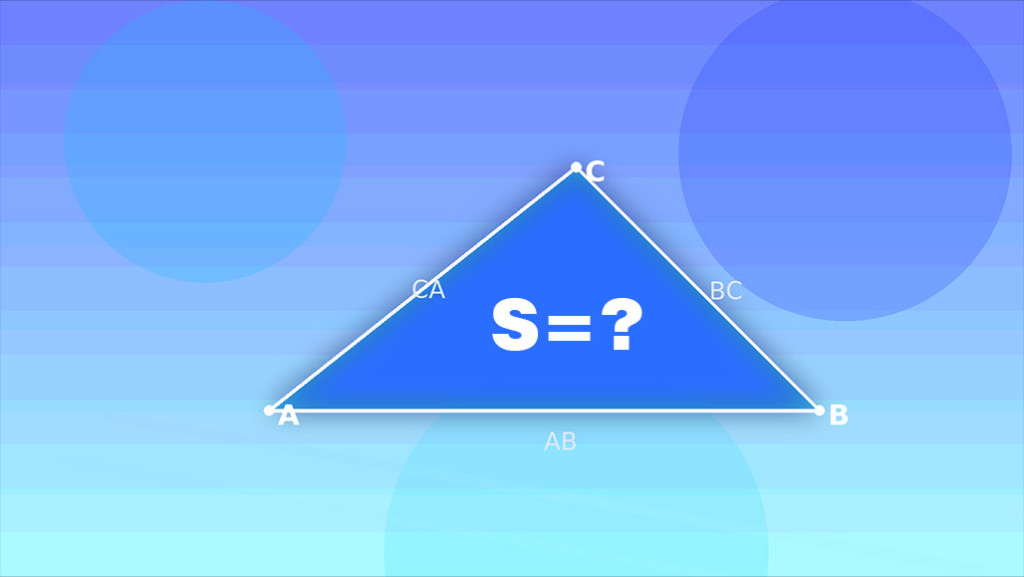
Online calculator voor de oppervlakte van een driehoek op basis van drie zijden (AB, BC, CA) met behulp van de formule van Heron. Het controleert de driehoeksongelijkheid, toont een proportioneel diagram met de hoekpunten A, B, C, en tekent een duidelijke “dakpoging” voor onmogelijke sets. Het diagram houdt de zijden in de juiste visuele proportie. Labels verschijnen op de randen (AB, BC, CA) en op de hoekpunten (A, B, C).
Driehoek Oppervlakte Calculator (3 Zijden)
Voer de lengtes van de zijden in AB, BC, CA. De oppervlakte (S) wordt berekend met de formule van Heron. Het diagram behoudt de juiste verhoudingen en labelt A, B, C en de zijden AB, BC, CA. Als de zijden geen driehoek kunnen vormen, wordt er een duidelijke “dakpoging” met de kloof getekend en zegt het resultaat “bestaat niet”.
Zijde AB
Zijde BC
Zijde CA
Oppervlakte (S)
Hoe te Gebruiken
- Voer drie positieve zijden in voor AB, BC, en CA.
- Druk op Bereken.
- Lees de oppervlakte S en bekijk de berekening en het diagram.
- Gebruik Decimalen om de afronding van het resultaat en de labels te regelen.
Opmerkingen: Als de zijden geen driehoek kunnen vormen, toont het resultaat “bestaat niet” en visualiseert het de langste zijde als de basis met twee stippellijnen die elkaar niet ontmoeten, waarbij de kloof wordt benadrukt.
Gebruik consistente eenheden voor alle zijden; de oppervlakte zal in die eenheden in het kwadraat zijn (m², cm², etc.).
Formules
Driehoeksongelijkheid (bestaan): AB + BC > CA, AB + CA > BC, BC + CA > AB (allemaal strikt).
Halve omtrek: s = (AB + BC + CA) / 2
Formule van Heron (oppervlakte): S = √[ s(s − AB)(s − BC)(s − CA) ]
- Equivalentie vorm: S = (1/4) √[(AB + BC + CA)(−AB + BC + CA)(AB − BC + CA)(AB + BC − CA)].
- Van oppervlakte naar hoogte op AB: hAB = 2S / AB (evenzo voor andere basissen).
- Met inradius r en omtrek R: S = r·s = (AB·BC·CA)/(4R).
- Gelijkzijdig (zijde a): S = (√3/4)·a².
Voorbeeldwaarden
| AB | BC | CA | Geldig? | Oppervlakte S |
| 3 | 4 | 5 | Ja | 6 |
| 5 | 5 | 6 | Ja | 12 |
| 7 | 5 | 6 | Ja | 14.6969 |
| 8 | 8 | 8 | Ja | 27.7128 |
| 10 | 6 | 8 | Ja | 24 |
| 9 | 12 | 15 | Ja | 54 |
| 2.5 | 4 | 5 | Ja | 4.9525 |
| 12 | 13 | 5 | Ja | 30 |
| 20 | 13 | 7 | Nee | — |
| 6.5 | 6.5 | 4.2 | Ja | 12.918 |
| 15 | 14 | 9 | Ja | 61.6441 |
| 30 | 29 | 10 | Ja | 144.6373 |
| 100 | 120 | 150 | Ja | 5981.168 |
| 1.2 | 1.3 | 2.4 | Ja | 0.4196 |
| 9 | 9 | 18 | Nee | — |
Interessante Feiten
- Resultaat van Heron: De formule is toegeschreven aan Heron van Alexandrië (1e eeuw na Christus) en heeft alleen de lengtes van de zijden nodig, geen hoeken of hoogtes.
- Heronische driehoeken: Driehoeken met gehele zijden en een gehele oppervlakte (bijv. 3-4-5 heeft S = 6) worden Heronisch genoemd.
- Maximale oppervlakte: Voor een vaste omtrek heeft de gelijkzijdige driehoek de grootste oppervlakte. Voor twee vaste zijden is de oppervlakte maximaal wanneer de ingesloten hoek 90° is.
- Degeneratie: Wanneer een som gelijk is aan de derde zijde (bijv. 20, 13, 7), valt de “driehoek” samen tot een segment en is S = 0.
- Controles: Van S en een basis zijn hoogtes, inradius (r = S/s), en omtrek (R = AB·BC·CA/(4S)) direct terug te halen.
CalcuLife.com


Laat een reactie achter