Arccos Calculator Online – Inverse Cosinus

Gebruik deze Arccos (inverse cosinus) calculator om de hoofdhoek θ te berekenen op basis van een cosinuswaarde x. De wiskunde achter de tool volgt de standaarddefinitie van de inverse cirkelvormige functies zoals gedocumenteerd door de Digitale Bibliotheek van Wiskundige Functies van NIST (zie Inverse Circulaire Functies op dlmf.nist.gov/4.23).

Dit delen?

Link kopiëren ✓

Hoe de arccos calculator werkt

1. Je voert een getal x in tussen −1 en 1.
2. De tool berekent θ = arccos(x) als de hoofdwaarde in radialen, en toont ook graden.
3. Het toont ook sin(θ) en een duidelijke eenheidscirkelvisualisatie van de straal, projecties en het punt.

Definitie en formule

Arccos retourneert de hoofdhoek θ die voldoet aan cos(θ) = x.

• Invoerdomein: x ∈ [−1, 1]
• Uitvoerbereik (hoofdwaarde): θ ∈ [0, π] radialen, wat overeenkomt met [0°, 180°]
• Conversie: graden = radialen × 180/π

Belangrijke identiteit: als cos(θ) = x, dan θ = arccos(x). Voor hoeken buiten het hoofdbereik bestaan er andere oplossingen: 2π − θ, enzovoort. Deze tool rapporteert de hoofdwaarde opzettelijk.

Invoer, uitvoer en precisie

• Geldige invoer x: elk reëel getal van −1 tot 1. Waarden buiten dit bereik zijn niet gedefinieerd voor reële hoeken.
• Hoekformaten: de tool toont zowel graden als radialen.
• Decimalen: gebruik de “Decimalen” controle om afronding in te stellen (0–10). Radialen profiteren vaak van 4–6 decimalen; graden zijn meestal goed met 2–4.

Snelle voorbeelden

• x = 1 → θ = 0 rad = 0°
• x = 0.5 → θ = arccos(0.5) = π/3 ≈ 1.0472 rad ≈ 60°
• x = 0 → θ = π/2 ≈ 1.5708 rad ≈ 90°
• x = −1 → θ = π ≈ 3.1416 rad = 180°

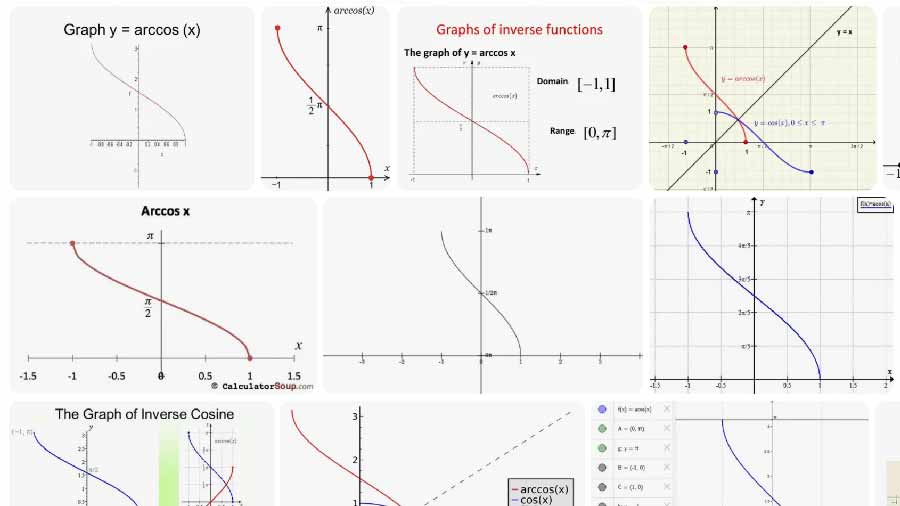
Eenheidscirkelinterpretatie

Op de eenheidscirkel (straal 1) is x de aanliggende zijde van de rechthoekige driehoek die is opgebouwd van de positieve x-as naar het punt op de cirkel, en √(1 − x²) is de tegenovergestelde zijde. Arccos retourneert de hoek θ die het punt plaatst op (x, √(1 − x²)) op de bovenste halve cirkel of (x, 0) op de uiteinden. Het canvas toont de straal naar dat punt en gestreepte projecties op de assen.

Veelvoorkomende toepassingen van arccos

• Hoek tussen vectoren: met genormaliseerde vectoren u en v, u·v = cos(θ) ⇒ θ = arccos(u·v).
• Geometrie en driehoeken: herleid een hoek uit de lengtes van de zijden via de Cosinusregel.
• Robotica en 3D-graphics: converteer inproduct naar hoeken voor verlichting, camera en poseberekeningen.
• Signaalverwerking: fase relaties en correlatiehoeken.

Nauwkeurigheid en afrondingsnotities

• Invoer met drijvende komma dicht bij ±1 kan afrondingsruis vergroten. Als een waarde zoals 1.0000001 verschijnt, beperk deze dan tot 1 voor een stabiel resultaat.
• Radialen hebben exacte eenvoudige vormen voor speciale hoeken (π/3, π/2, π). De decimale weergave toont afgeronde benaderingen.
• Als je maximale precisie nodig hebt, verhoog dan de decimalencontrole en lees de radiale waarde.

FAQ

Is arccos hetzelfde als cos⁻¹?
Ja. cos⁻¹(x) betekent de inverse functie arccos(x), niet 1/cos(x).

Waarom weigert de calculator waarden kleiner dan −1 of groter dan 1?
Voor reële hoeken is de cosinus beperkt tot [−1, 1]. Invoeren buiten dat interval hebben geen reële arccos.

Waarom krijg ik maar één hoek?
De calculator retourneert de hoofdwaarde in [0, π]. Andere co-terminal of supplementaire hoeken bestaan, maar de hoofdvertakking is standaard voor inverse trigonometrische functies en houdt de resultaten voorspelbaar.

Moet ik graden of radialen gebruiken?
Gebruik graden voor dagelijkse interpretatie en radialen voor calculus, natuurkunde en de meeste programmeerbibliotheken.

Wat is jouw reden om deze calculator te gebruiken? Zou je andere tools of functies willen? Laat het ons weten in de reacties!

CalcuLife.com