Calculatrice de Arctangente en Ligne – Simple et Précise

Notre Calculatrice de Arctangente est un outil en ligne simple conçu pour calculer l’arctangente de tout nombre donné. Ce calculateur est particulièrement utile pour les étudiants, les éducateurs et les professionnels qui ont besoin de déterminer rapidement l’angle correspondant à une valeur de tangente en trigonométrie.

Comment Utiliser la Calculatrice

Utiliser la calculatrice est simple :

1. Entrez n’importe quel nombre dans le champ de saisie. Il n’y a aucune restriction sur la gamme de valeurs que vous pouvez entrer.
2. Cliquez sur ‘Calculer Arctangente’ pour obtenir l’arctangente de la valeur entrée.
3. La calculatrice affichera le résultat à la fois en degrés et en radians.
4. Si vous souhaitez effectuer un autre calcul, cliquez sur ‘Effacer’ pour réinitialiser la calculatrice.

Comprendre la Formule et les Calculs

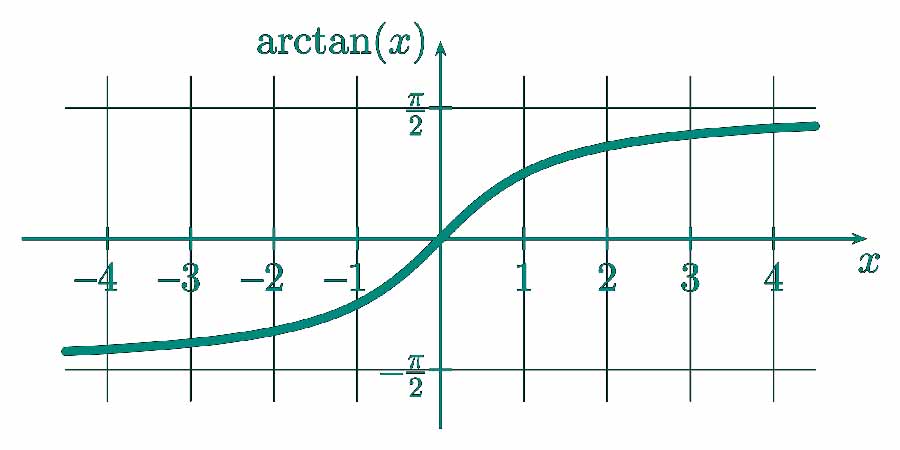
La fonction arctangente, également connue sous le nom de tan⁻¹, est l’inverse de la fonction tangente. Elle trouve l’angle dont la tangente est le nombre donné. La formule appliquée est :

• arctangente(x) = tan⁻¹(x)

Pour toute valeur ‘x’, arctangente(x) renvoie l’angle, généralement mesuré en radians ou en degrés. La plage standard pour arctangente est de -π/2 à π/2 radians (ou -90° à 90° en degrés).

Informations Éducatives sur l’Arctangente

Le concept d’arctangente est fondamental en trigonométrie et est essentiel pour comprendre la relation entre les angles et les rapports des côtés dans les triangles rectangles. Il est indispensable pour résoudre des problèmes impliquant des pentes, des angles d’élévation ou de dépression, et pour analyser des motifs d’ondes en physique.

Dans les applications réelles, l’arctangente est vitale dans des domaines tels que l’ingénierie, où elle aide à concevoir des structures en calculant des angles de soutien. En navigation et en astronomie, elle aide à déterminer les positions et les trajectoires. La graphique par ordinateur et le développement de jeux utilisent également l’arctangente pour rendre des objets 3D et calculer des angles de vue.

Comprendre l’arctangente est crucial pour quiconque se plonge dans des domaines impliquant la géométrie, la physique ou toute discipline où les angles et leurs mesures sont importants. Cette calculatrice simplifie ces calculs complexes, facilitant la compréhension et l’application de ces concepts.

© CalcuLife.com