Calculatrice Arcsin en Ligne – Précise et Facile à Utiliser

Notre Calculatrice Arcsin est un outil convivial conçu pour calculer l’arcsinus (sinus inverse) d’un nombre donné. C’est un outil essentiel pour les étudiants, les éducateurs et les professionnels en mathématiques, physique et ingénierie, fournissant des résultats rapides et précis tant en degrés qu’en radians.

Comment Utiliser la Calculatrice

Pour utiliser la calculatrice, entrez une valeur numérique entre -1 et 1 dans le champ de saisie. Cliquez sur ‘Calculer Arcsin’ pour recevoir l’arcsinus de la valeur entrée. La calculatrice affiche le résultat en degrés et en radians, accompagné d’un processus de calcul détaillé. Pour réinitialiser ou effectuer de nouveaux calculs, utilisez le bouton ‘Effacer’, qui efface toutes les entrées et sorties.

Comprendre la Formule et les Calculs

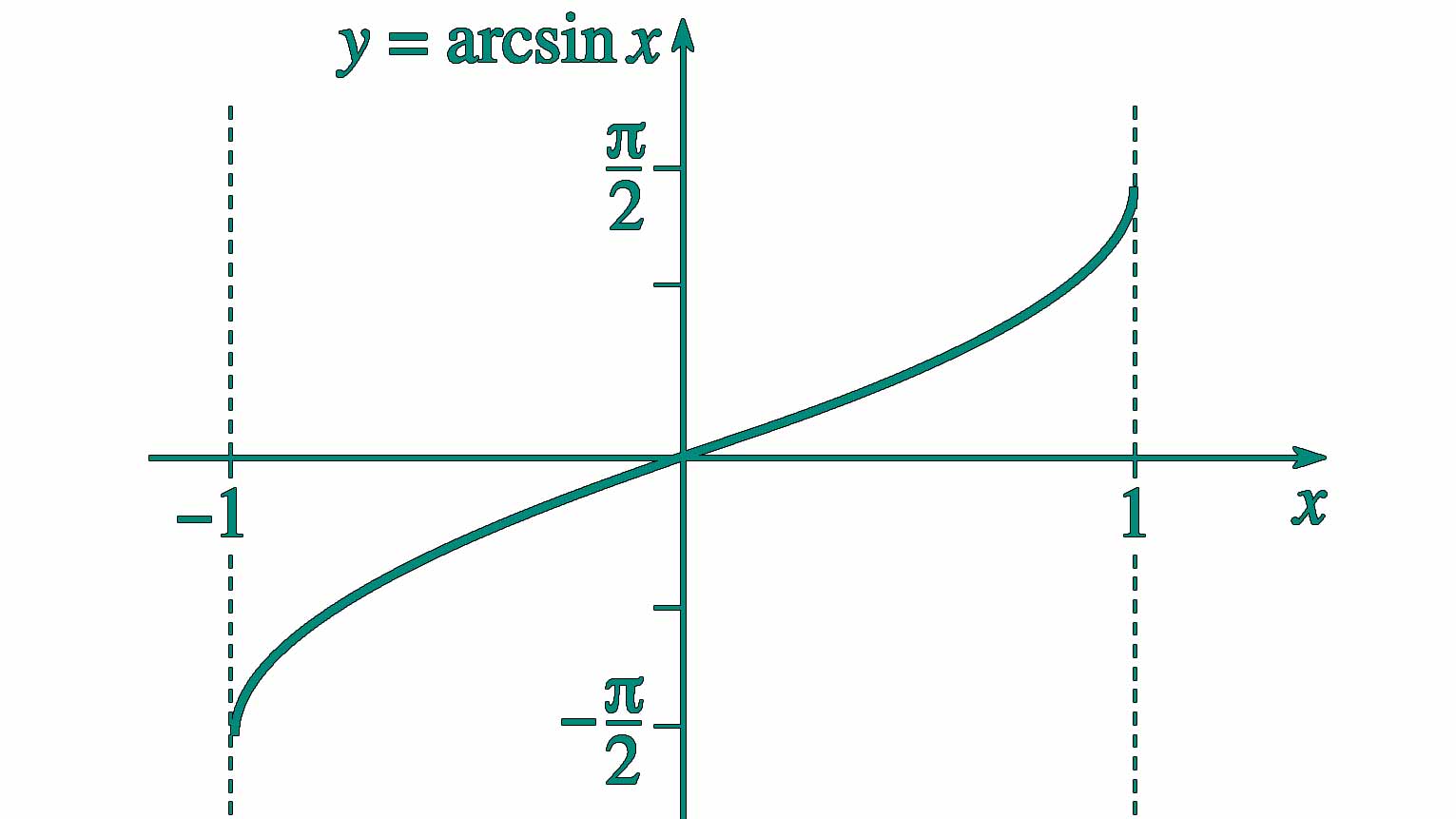
La fonction arcsinus, notée Arcsin ou sin⁻¹, est l’inverse de la fonction sinus. La formule utilisée est :

• Arcsin(x) = sin⁻¹(x)

Pour une valeur ‘x’, Arcsin(x) renvoie l’angle dont le sinus est ‘x’. La plage de sortie standard pour Arcsin est entre -π/2 et π/2 radians (ou -90° et 90° en degrés).

Cependant, notre calculatrice affiche également l’angle supplémentaire, qui est de 180° moins la valeur d’Arcsin en degrés ou π moins la valeur d’Arcsin en radians. Ces angles supplémentaires offrent des perspectives supplémentaires sur la solution.

Apports Pédagogiques

Arcsin joue un rôle essentiel dans la résolution de problèmes impliquant des triangles rectangles, des fonctions d’onde et des oscillations harmoniques. La calculatrice aide non seulement à résoudre des problèmes mathématiques, mais aide également à visualiser le concept de fonctions trigonométriques inverses et leurs applications pratiques. Apprendre à interpréter à la fois les angles principaux et supplémentaires peut améliorer les compétences de résolution de problèmes, en particulier dans les contextes physiques et d’ingénierie où différents angles peuvent produire des résultats fonctionnellement équivalents.