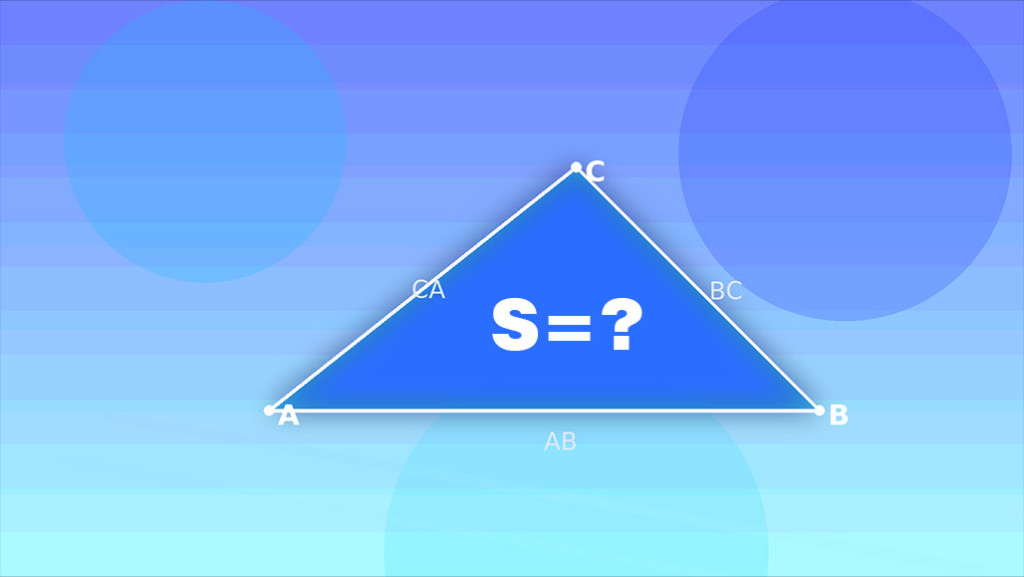
Esta calculadora en línea obtiene el área de un triángulo a partir de tres longitudes de lados (AB, BC, CA) usando la fórmula de Herón. Verifica la desigualdad del triángulo, muestra un diagrama proporcional con los vértices A, B, C y dibuja un “intento de techo” cuando los lados son imposibles. El diagrama mantiene las longitudes en proporción visual correcta. Las etiquetas aparecen en los lados (AB, BC, CA) y en los vértices (A, B, C).
Calculadora de Área de Triángulo (3 lados)
Ingrese las longitudes de los lados AB, BC, CA. El área (S) se calcula con la fórmula de Herón. El diagrama mantiene proporciones reales y muestra A, B, C y los lados AB, BC, CA. Si no forman triángulo, se dibuja un “techo” con la brecha y el resultado indica “no existe”.
Lado AB
Lado BC
Lado CA
Área (S)
Cómo usarla
- Ingresa tres longitudes positivas para AB, BC y CA.
- Haz clic en Calcular.
- Lee el área S y revisa el procedimiento y el diagrama.
- Usa Decimales para controlar el redondeo del resultado y de las etiquetas.
Notas: Si los lados no pueden formar un triángulo, el resultado muestra “no existe” y la visualización dibuja el lado más largo como base con dos brazos punteados que no se unen, resaltando el espacio.
Usa las mismas unidades en todos los lados; el área se dará en esas unidades al cuadrado (m², cm², in², ft², etc.).
Fórmulas
Desigualdad del triángulo (existencia): AB + BC > CA, AB + CA > BC, BC + CA > AB (todas estrictas).
Semiperímetro: s = (AB + BC + CA) / 2
Fórmula de Herón (área): S = √[ s(s − AB)(s − BC)(s − CA) ]
- Forma equivalente: S = (1/4) √[(AB + BC + CA)(−AB + BC + CA)(AB − BC + CA)(AB + BC − CA)].
- De área a altura sobre AB: hAB = 2S / AB (igual para otras bases).
- Con inradio r y circunradio R: S = r·s = (AB·BC·CA)/(4R).
- Equilátero (lado a): S = (√3/4)·a².
Ejemplos
| AB | BC | CA | ¿Válido? | Área S |
| 3 | 4 | 5 | Sí | 6 |
| 5 | 5 | 6 | Sí | 12 |
| 7 | 5 | 6 | Sí | 14.6969 |
| 8 | 8 | 8 | Sí | 27.7128 |
| 10 | 6 | 8 | Sí | 24 |
| 9 | 12 | 15 | Sí | 54 |
| 2.5 | 4 | 5 | Sí | 4.9525 |
| 12 | 13 | 5 | Sí | 30 |
| 20 | 13 | 7 | No | — |
| 6.5 | 6.5 | 4.2 | Sí | 12.918 |
| 15 | 14 | 9 | Sí | 61.6441 |
| 30 | 29 | 10 | Sí | 144.6373 |
| 100 | 120 | 150 | Sí | 5981.168 |
| 1.2 | 1.3 | 2.4 | Sí | 0.4196 |
| 9 | 9 | 18 | No | — |
Datos interesantes
- Resultado de Herón: La fórmula se atribuye a Herón de Alejandría (siglo I d.C.) y solo requiere las longitudes de los lados, sin ángulos ni alturas.
- Triángulos heronianos: Triángulos con lados enteros y área entera (ej. 3-4-5 con S = 6) se llaman heronianos.
- Área máxima: Para un perímetro fijo, el triángulo equilátero tiene el área más grande. Para dos lados fijos, el área es máxima cuando el ángulo incluido es de 90°.
- Degeneración: Cuando la suma de dos lados es igual al tercero (ej. 20, 13, 7), el “triángulo” colapsa en un segmento y S = 0.
- Comprobaciones: A partir de S y una base se pueden obtener directamente las alturas, el inradio (r = S/s) y el circunradio (R = AB·BC·CA/(4S)).
CalcuLife.com







Deja tu comentario