Calculadora Arccos en Línea – Coseno Inverso

Utiliza esta calculadora de Arcoseno (coseno inverso) para obtener el ángulo principal θ a partir de un valor de coseno x. La matemática detrás de la herramienta sigue la definición estándar de las funciones circulares inversas, como se documenta en la Biblioteca Digital de Funciones Matemáticas del NIST (ver Funciones Circulares Inversas en dlmf.nist.gov/4.23).

¿Compartir esto?

Copiar enlace ✓

Cómo funciona la calculadora de arcoseno

1. Ingresas un número x entre −1 y 1.
2. La herramienta calcula θ = arcos(x) como el valor principal en radianes, y luego muestra los grados también.
3. También muestra sin(θ) y una visualización limpia del círculo unitario con el radio, proyecciones y el punto.

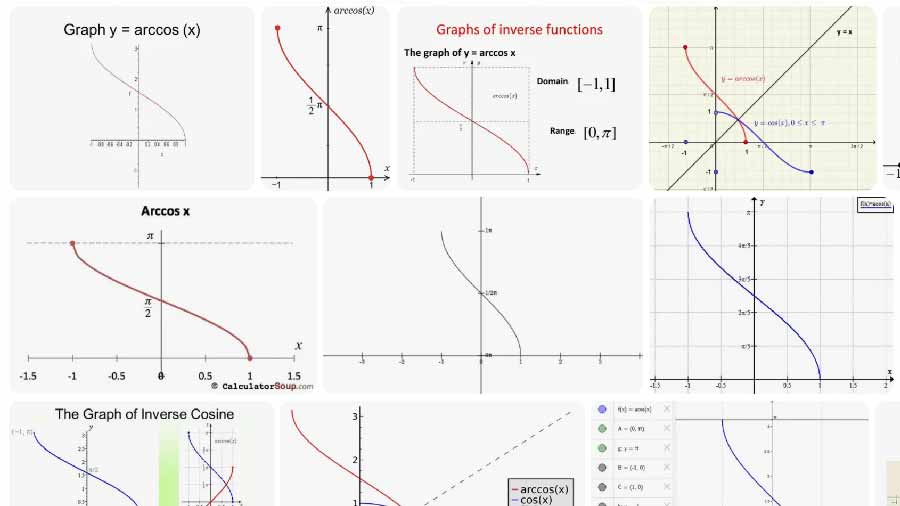
Definición y fórmula

El arcoseno devuelve el ángulo principal θ que satisface cos(θ) = x.

• Dominio de entrada: x ∈ [−1, 1]
• Rango de salida (valor principal): θ ∈ [0, π] radianes, que es [0°, 180°]
• Conversión: grados = radianes × 180/π

Identidad clave: si cos(θ) = x, entonces θ = arcos(x). Para ángulos fuera del rango principal, existen otras soluciones: 2π − θ, etc. Esta herramienta reporta el valor principal por diseño.

Entradas, salidas y precisión

• Entrada válida x: cualquier número real de −1 a 1. Los valores fuera de este rango no están definidos para ángulos reales.
• Formatos de ángulo: la herramienta muestra tanto grados como radianes.
• Decimales: utiliza el control de “Decimales” para establecer el redondeo (0–10). Los radianes a menudo se benefician de 4–6 decimales; los grados comúnmente están bien con 2–4.

Ejemplos rápidos

• x = 1 → θ = 0 rad = 0°
• x = 0.5 → θ = arcos(0.5) = π/3 ≈ 1.0472 rad ≈ 60°
• x = 0 → θ = π/2 ≈ 1.5708 rad ≈ 90°
• x = −1 → θ = π ≈ 3.1416 rad = 180°

Interpretación del círculo unitario

En el círculo unitario (radio 1), x es el lado adyacente del triángulo rectángulo construido desde el eje x positivo hasta el punto en el círculo, y √(1 − x²) es el lado opuesto. El arcoseno devuelve el ángulo θ que coloca el punto en (x, √(1 − x²)) en el semicírculo superior o (x, 0) en los extremos. El lienzo muestra el radio hasta ese punto y proyecciones discontinuas sobre los ejes.

Usos comunes del arcoseno

• Ángulo entre vectores: con vectores normalizados u y v, u·v = cos(θ) ⇒ θ = arcos(u·v).
• Geometría y triángulos: recuperar un ángulo a partir de las longitudes de los lados mediante la Ley de los Cosenos.
• Robótica y gráficos 3D: convertir productos punto en ángulos para cálculos de iluminación, cámara y pose.
• Procesamiento de señales: relaciones de fase y ángulos de correlación.

Notas sobre precisión y redondeo

• La entrada de punto flotante cerca de ±1 puede magnificar el ruido de redondeo. Si aparece un valor como 1.0000001, restríngelo a 1 para un resultado estable.
• Los radianes tienen formas simples exactas para ángulos especiales (π/3, π/2, π). La visualización decimal mostrará aproximaciones redondeadas.
• Si necesitas la máxima precisión, aumenta el control de decimales y lee el valor en radianes.

Preguntas frecuentes

¿Es el arcoseno lo mismo que cos⁻¹?
Sí. cos⁻¹(x) significa la función inversa arcos(x), no 1/cos(x).

¿Por qué la calculadora rechaza valores menores que −1 o mayores que 1?
Para ángulos reales, el coseno está limitado a [−1, 1]. Las entradas fuera de ese intervalo no tienen arcoseno real.

¿Por qué solo obtengo un ángulo?
La calculadora devuelve el valor principal en [0, π]. Existen otros ángulos coterminales o suplementarios, pero la rama principal es estándar para funciones trigonométricas inversas y mantiene los resultados predecibles.

¿Debería usar grados o radianes?
Usa grados para la interpretación diaria y radianes para cálculo, física y la mayoría de las bibliotecas de programación.

¿Cuál es tu caso de uso de esta calculadora? ¿Te gustaría alguna otra herramienta o función? ¡Háznoslo saber en los comentarios!

CalcuLife.com