Volumenrechner für abgeschnittene Pyramiden

Dieser Online-Rechner berechnet das Volumen eines abgeschnittenen Pyramidenstumpfs (Frustum) für sowohl quadratische als auch rechteckige Basen. Er implementiert die standardmäßige Formel für das Volumen eines Frustums mit konsistenter Einheitshandhabung und Präzisionskontrolle. Die Methode basiert auf klassischer Geometrie (siehe Frustum – Volumen), sodass die Ergebnisse mathematisch zuverlässig sind, wenn die Eingaben gültig sind (nicht-negative Dimensionen mit Ober-/Unterseite in derselben Einheit). Dieses Werkzeug ist besonders nützlich für Ingenieure und Architekten in Deutschland, die präzise Berechnungen für ihre Projekte benötigen.

Volumenrechner für truncierte Pyramiden

Was Sie eingeben werden

Unterseite a

Oberseite b

Höhe h

Einheit

Dezimalstellen

Volumen

—

Eingaben Zusammenfassung

Formel

V = (h / 3) · (A_unten + A_oben + √(A_unten · A_oben))
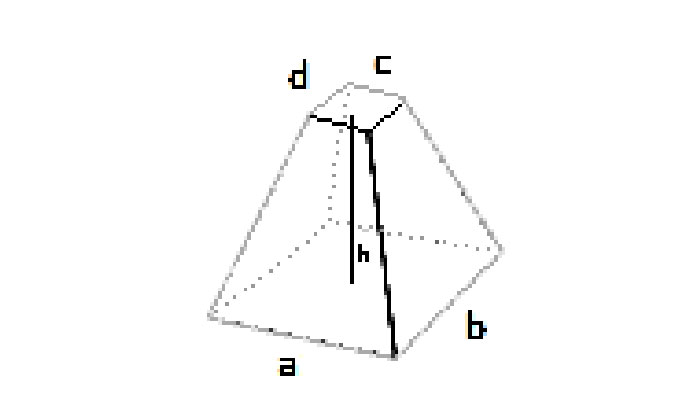
Quadrat: A_unten=a², A_oben=b² ⇒ V = (h/3)(a² + b² + ab)
Rechteckig: A_unten=L₁·W₁, A_oben=L₂·W₂

Die Visualisierung verwendet eine feste axonometrische Projektion: Die oberen und unteren Rechtecke bleiben parallel und zentriert; die vertikalen Kanten skalieren mit Ihrer Höhe. Hilfslinien markieren L (blau), W (grün) und h (rot).

Das hier teilen?

So verwenden Sie es

Wählen Sie den Modus Quadratisch, Rechteckig oder Flächen.
Geben Sie ein:
- Quadratisch: Unterseite a, Oberseite b, Höhe h.
- Rechteckig: Unterseite L₁ × W₁, Oberseite L₂ × W₂, Höhe h.
- Flächen: Untere Fläche A_bottom, obere Fläche A_top, Höhe h.
Wählen Sie die Einheit und die Dezimalgenauigkeit aus und klicken Sie dann auf Berechnen.
Die Visualisierung spiegelt Ihre Proportionen wider: blau ≈ Länge (L), grün ≈ Breite (W), rot ≈ Höhe (h). Die Pille unten zeigt Ihre Eingaben zum Kopieren/Einfügen an.

Formeln

Allgemeines Volumen eines Frustums

V = (h / 3) · (A_bottom + A_top + √(A_bottom · A_top))

Quadratische Basen (Unterseite a, Oberseite b):
A_bottom = a², A_top = b² ⇒ V = (h / 3) · (a² + b² + a·b)

Rechteckige Basen (Unterseite L₁×W₁, Oberseite L₂×W₂):
A_bottom = L₁·W₁, A_top = L₂·W₂ ⇒ V = (h / 3) · (L₁W₁ + L₂W₂ + √(L₁W₁·L₂W₂))

Überprüfungen der Plausibilität. Wenn die Oberseite gleich der Unterseite ist (A_top = A_bottom), wird die Form zu einem Prisma und V = A_bottom·h. Wenn die Oberseite 0 ist, handelt es sich um eine vollständige Pyramide und V = (A_bottom·h)/3.

Vorkalkulierte Beispiele (alle Eingaben in cm; Volumen in cm³)

Modus	Unterdimensionen	Oberdimensionen	h	Volumen
Quadratisch	a × a = 10 × 10	b × b = 6 × 6	12	784
Quadratisch	a × a = 5 × 5	b × b = 5 × 5	8	200
Quadratisch	a × a = 20 × 20	b × b = 10 × 10	15	3.500
Quadratisch	a × a = 7.5 × 7.5	b × b = 3.2 × 3.2	18	542,94
Rechteckig	L₁×W₁ = 12 × 8	L₂×W₂ = 6 × 4	20	1.120
Rechteckig	L₁×W₁ = 50 × 40	L₂×W₂ = 30 × 20	35	43.113,5263
Rechteckig	L₁×W₁ = 15 × 10	L₂×W₂ = 15 × 5	12	1.324,2641

Alle Werte wurden doppelt überprüft mit V = (h/3)(A_bottom + A_top + √(A_bottomA_top)). Rundungen werden auf 2–4 Dezimalstellen angezeigt, wo hilfreich.

Praktische Tipps & Qualitätsprüfungen

Einheiten konsistent halten. Geben Sie alle linearen Dimensionen in derselben Einheit ein; der Rechner konvertiert das Volumen in dieser Einheit³ (z. B. cm → cm³).
Höhe korrekt messen. Verwenden Sie den rechtwinkligen Abstand zwischen den Basen (nicht eine schräge Kante).
Verwenden Sie den Flächenmodus, wenn Sie bereits die Basisflächen kennen (aus Zeichnungen, CAD oder Baustellenmessungen), um kumulative Rundungsfehler zu vermeiden.
Plausibilitätsprüfung mit Extremen: Wenn b → a, sollte das Ergebnis A·h annähern. Wenn b → 0, sollte das Ergebnis (A·h)/3 annähern.
Präzisionskontrolle: Erhöhen Sie „Dezimalstellen“, wenn die Eingaben klein sind oder wenn Sie planen, Berechnungen zu verketten (z. B. zu Masse unter Verwendung der Dichte).

CalcuLife.com