Der Ball ist eine der grundlegenden geometrischen Formen. Im wirklichen Leben findet man selten perfekt geformte Bälle, aber in der Schule oder an der Universität kann es vorkommen, dass man die Aufgabe hat, das Volumen eines Balls zu berechnen. Entweder müssen Sie Bälle für Lager herstellen oder das Volumen von Basketballen berechnen. Wir empfehlen Ihnen, unseren einfachen und schnellen Volumenrechner für Bälle zu verwenden. Sie können das Ergebnis auch in die gewünschte Volumeneinheit umrechnen.
Verwenden Sie diesen Online-Rechner, um das Volumen einer Kugel aus dem Radius oder Durchmesser zu berechnen. Die Ergebnisse erscheinen in cm³, m³, in³ und ft³. Unterstützte Längeneinheiten: Zentimeter (cm), Meter (m), Zoll (in), Fuß (ft). Unterstützte Volumeneinheiten: Kubikzentimeter (cm³), Kubikmeter (m³), Kubikzoll (in³), Kubikfuß (ft³).
So verwenden Sie es
- Wählen Sie Messart (Radius oder Durchmesser).
- Geben Sie den numerischen Wert ein und wählen Sie seine Einheit (cm, m, in, ft).
- Klicken Sie auf Berechnen. Die Anzeige kennzeichnet die gewählte Dimension; das Ergebnisfeld zeigt das Volumen in allen Einheiten sowie Radius, Durchmesser, Umfang und Oberfläche an.
- Verwenden Sie Ergebnisse kopieren, um den zusammenfassenden Text zu kopieren. Die Schaltfläche wird nach einer gültigen Berechnung aktiviert.
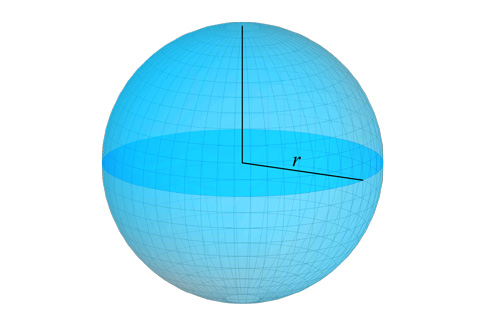
Der Radius eines Balls ist der Abstand von seinem Zentrum zu seinem Rand
Definitionen der Einheiten
- Zentimeter (cm) — SI-Längeneinheit. 1 m = 100 cm. Exakte Beziehung zu Zoll: 1 in = 2,54 cm (exakt).
- Meter (m) — SI-Basiseinheit für Länge. 1 m = 39,3700787402 in (abgeleitet von 1 in = 2,54 cm exakt) und 1 m = 3,280839895 ft. Für Volumen gilt: 1 m³ = 1.000.000 cm³ und 1 m³ = 1.000 L.
- Zoll (in) — US-amerikanische/imperiale Längeneinheit. Genau definiert als 1 in = 2,54 cm. 12 in = 1 ft.
- Fuß (ft) — US-amerikanische/imperiale Längeneinheit. 1 ft = 12 in = 0,3048 m (exakt). 1 ft³ = 1728 in³.
- Kubikzentimeter (cm³) — SI-abgeleitete Volumeneinheit. 1 cm³ = 1 mL. Exakte Beziehung: 1 in³ = 16,387064 cm³.
- Kubikmeter (m³) — SI-Basiseinheit für Volumen. 1 m³ = 35,3146667 ft³ = 61.023,7441 in³ (exakte Faktoren).
- Kubikzoll (in³) — US-amerikanische/imperiale Volumeneinheit. Exakte Beziehung: 1 in³ = 16,387064 cm³.
- Kubikfuß (ft³) — US-amerikanische/imperiale Volumeneinheit. 1 ft³ = 1728 in³ = 0,028316846592 m³ (exakt).
Formel
Das Volumen einer Kugel verwendet die Formel V = (4/3)·π·r³. Wenn der Durchmesser d gegeben ist, dann ist r = d/2; der Umfang auf einem großen Kreis ist C = 2·π·r; die Oberfläche ist A = 4·π·r². Referenz: Wolfram MathWorld — Kugel.
Referenztabelle (Radius in cm → Volumen)
| Radius (cm) | Volumen (cm³) | Volumen (m³) | Volumen (in³) |
|---|---|---|---|
| 0.50 | 0.524 | 0.000001 | 0.032 |
| 1.00 | 4.189 | 0.000004 | 0.256 |
| 1.50 | 14.137 | 0.000014 | 0.863 |
| 2.00 | 33.510 | 0.000034 | 2.045 |
| 2.50 | 65.450 | 0.000065 | 3.994 |
| 3.00 | 113.097 | 0.000113 | 6.902 |
| 4.00 | 268.083 | 0.000268 | 16.359 |
| 5.00 | 523.599 | 0.000524 | 31.952 |
| 6.00 | 904.779 | 0.000905 | 55.213 |
| 7.50 | 1767.146 | 0.001767 | 107.838 |
| 10.00 | 4188.790 | 0.004189 | 255.616 |
| 12.50 | 8181.231 | 0.008181 | 499.249 |
| 15.00 | 14137.167 | 0.014137 | 862.703 |
| 20.00 | 33510.322 | 0.033510 | 2044.925 |
| 25.00 | 65449.847 | 0.065450 | 3993.995 |
| 30.00 | 113097.336 | 0.113097 | 6901.623 |
| 35.00 | 179594.380 | 0.179594 | 10959.521 |
| 40.00 | 268082.573 | 0.268083 | 16359.402 |
| 50.00 | 523598.776 | 0.523599 | 31951.958 |
| 60.00 | 904778.684 | 0.904779 | 55212.983 |
Reale Beispiele für das Volumen von Bällen
- Tischtennisball, Durchmesser 40,0 mm — Volumen 33,510 cm³ und 2,045 in³.
- Krocketball, Durchmesser 92,0 mm — Volumen 407,720 cm³ und 24,881 in³.
- Kaugummiball, Durchmesser 25,4 mm (Standardgröße) — Volumen 8,580 cm³ und 0,524 in³.
- Sphärischer Eisball, Durchmesser 63,5 mm (gängig in Bars) — Volumen 134,066 cm³ und 8,181 in³.
- Weihnachtsbaumkugel, Durchmesser 80,0 mm (gängig im Einzelhandel) — Volumen 268,083 cm³ und 16,359 in³.
- Murmel, Durchmesser 12,7 mm (kleine Größe) — Volumen 1,073 cm³ und 0,065 in³.
- Murmel, Durchmesser 16,0 mm (5/8-Zoll-Klasse) — Volumen 2,145 cm³ und 0,131 in³.
- Sphärische Kerze, Durchmesser 76,2 mm — Volumen 231,667 cm³ und 14,137 in³.
- Billardball, Durchmesser 57,15 mm — Volumen 97,734 cm³ und 5,964 in³.
- Snookerball, Durchmesser 52,5 mm — Volumen 75,766 cm³ und 4,624 in³.
Was ist Ihr Szenario für diesen Rechner? Benötigen Sie andere Online-Tools? Lassen Sie es uns in den Kommentaren wissen, und wir werden es einrichten.
CalcuLife.com






Hinterlasse einen Kommentar