Калькулятор площади трапеции находит площадь трапеции по ее двум основаниям и высоте, используя стандартную геометрическую формулу. Единственные входные данные, которые вам нужны, это длины верхнего основания a, нижнего основания b и перпендикулярной высоты h. Визуализация центрируется и масштабируется под ваши числа, чтобы вы могли видеть, какая сторона какая. Этот инструмент особенно полезен для студентов и профессионалов в России, где геометрия играет важную роль в образовании и строительстве.

Калькулятор площади трапеции
h=0 a=0 b=0
Поделиться этим?
WhatsApp X Telegram Facebook LinkedIn Reddit

Как работает калькулятор

  • Входные данные: Верхнее основание a, нижнее основание b, высота h (все положительные действительные числа).
  • Формула: Площадь = ((a + b) / 2) × h. Для краткой справки по формуле смотрите Wolfram MathWorld: Трапеция.
  • Единицы измерения: Результат выводится в квадратных единицах. Если входные данные в метрах, результат будет в м²; если в дюймах, то в дюймах². Инструмент оставляет единицы измерения общими, чтобы подходить для любого контекста.
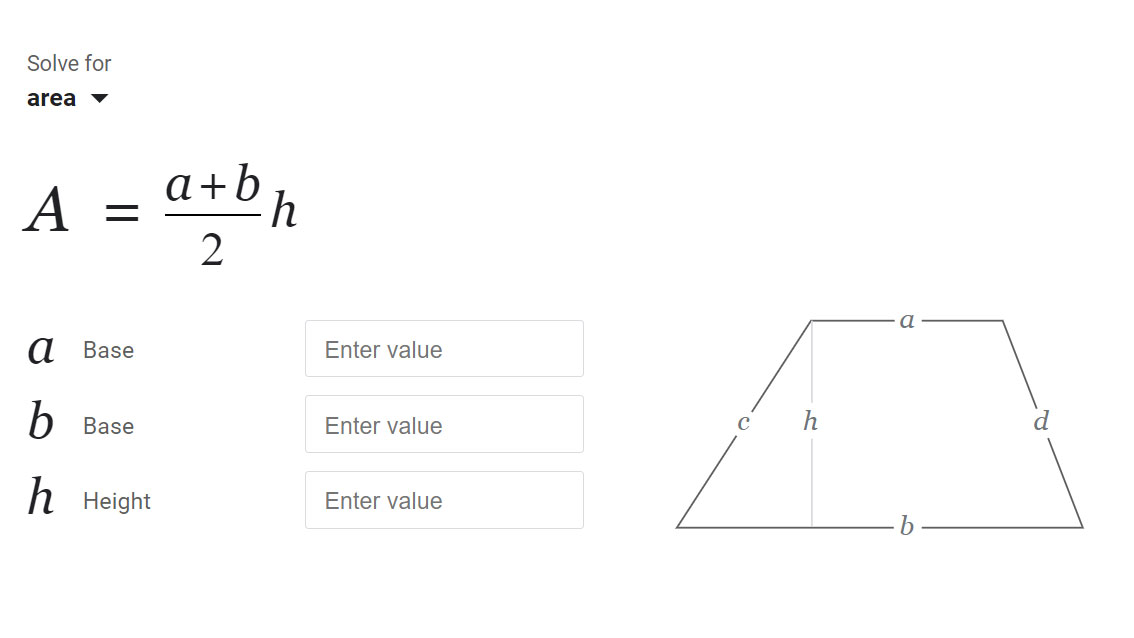
  • Визуализация: Диаграмма всегда остается в центре холста и подписывает те же величины, которые вы ввели: a сверху, b снизу и h как перпендикулярное расстояние между ними.
  • Числовая стабильность: Инструмент принимает десятичные дроби, большие и маленькие значения. Он округляет отображение аккуратно, сохраняя внутреннюю точность.

Почему эта формула верна

Площадь трапеции равна высоте, умноженной на среднее двух параллельных сторон. Интуитивно, если вы “сдвинете” короткое основание вдоль высоты, вы можете преобразовать трапецию в прямоугольник, ширина которого равна среднему значению двух оснований. Это дает A = h × (a + b)/2.

Калькулятор площади трапеции с визуализацией

Пошаговые примеры

  1. Пример 1 (соответствует стандартному рисунку):
    • a = 6, b = 10, h = 4
    • Среднее оснований = (6 + 10)/2 = 8
    • Площадь = 8 × 4 = 32 квадратных единиц
  2. Пример 2 (десятичные дроби):
    • a = 3.5, b = 12, h = 2.8
    • Среднее оснований = (3.5 + 12)/2 = 7.75
    • Площадь = 7.75 × 2.8 = 21.7 квадратных единиц
  3. Пример 3 (узкая высота):
    • a = 20, b = 24, h = 0.5
    • Среднее оснований = 22
    • Площадь = 22 × 0.5 = 11 квадратных единиц

Обратные вычисления, которые могут понадобиться

  • Решить для высоты при заданной площади и основаниях:
    h = (2 × Площадь) / (a + b)
  • Решить для неизвестного основания при заданной площади, другом основании и высоте:
    a = (2 × Площадь) / h − b (или поменять a и b)

Что считается высотой

Высота перпендикулярна основаниям. Это не наклонная сторона. Если стороны наклонены, высота все равно остается кратчайшим прямым расстоянием между двумя основаниями. В прямоугольных или равнобедренных трапециях это легко увидеть; в тупоугольных случаях она остается перпендикулярной.

Проверка качества и крайние случаи

  • Положительность: Все три входных значения должны быть больше нуля, чтобы получить площадь.
  • Равные основания: Если a = b, трапеция становится прямоугольником; формула сводится к A = b × h, как и ожидалось.
  • Очень большие или очень маленькие числа: Площадь масштабируется линейно с высотой и со средним значением оснований. Удвоение каждого входного значения удваивает площадь для высоты и удваивает для среднего оснований, как это уместно.

Формы трапеций в реальном мире

  • Поперечные сечения дорог и median: Обочины и насыпи часто образуют трапеции, когда их рассматривают сбоку.
  • Конструкция крыш: Некоторые панели с двускатной или односкатной крышей, а также профили карнизов, имеют трапециевидную форму.
  • Ландшафтные клумбы и пандусы: Плановые виды и боковые профили часто дают трапеции.
  • Детали из листового металла и плитки: Трапециевидные заготовки распространены в производстве и укладке полов.
  • Канавы и каналы: Инженерные поперечные сечения канав часто используют трапециевидные профили.

Использование результата

  • Оценка материалов: Умножьте площадь на толщину, чтобы приблизительно оценить объем (например, почвы или бетона). Соблюдайте единообразие единиц измерения.
  • Смета: Если материал оценивается за квадратную единицу, умножьте стоимость единицы на вашу площадь, чтобы оценить расходы.
  • Масштабирование чертежей: Если ваши входные данные были получены из масштабированного плана, преобразуйте в реальные единицы измерения перед расчетом площади.

Распространенные ошибки, которых следует избегать

  • Использование наклонной стороны вместо перпендикулярной высоты.
  • Неправильное добавление единиц измерения. Держите все входные данные в одной и той же единице, чтобы вывод был в квадрате этой единицы.
  • Забывание о том, что формула использует среднее оснований, а не их разницу.

CalcuLife.com