De trapeziumoppervlaktecalculator vindt de oppervlakte van een trapezium op basis van zijn twee bases en hoogte met behulp van de standaard geometrische formule. De enige invoer die je nodig hebt, zijn de lengtes van de bovenste basis a, de onderste basis b, en de loodrechte hoogte h. De visualisatie centreert en schaalt naar jouw getallen, zodat je kunt zien welke kant welke is. Dit hulpmiddel is bijzonder nuttig voor studenten en professionals in Nederland die met geometrie werken.
Hoe de calculator werkt
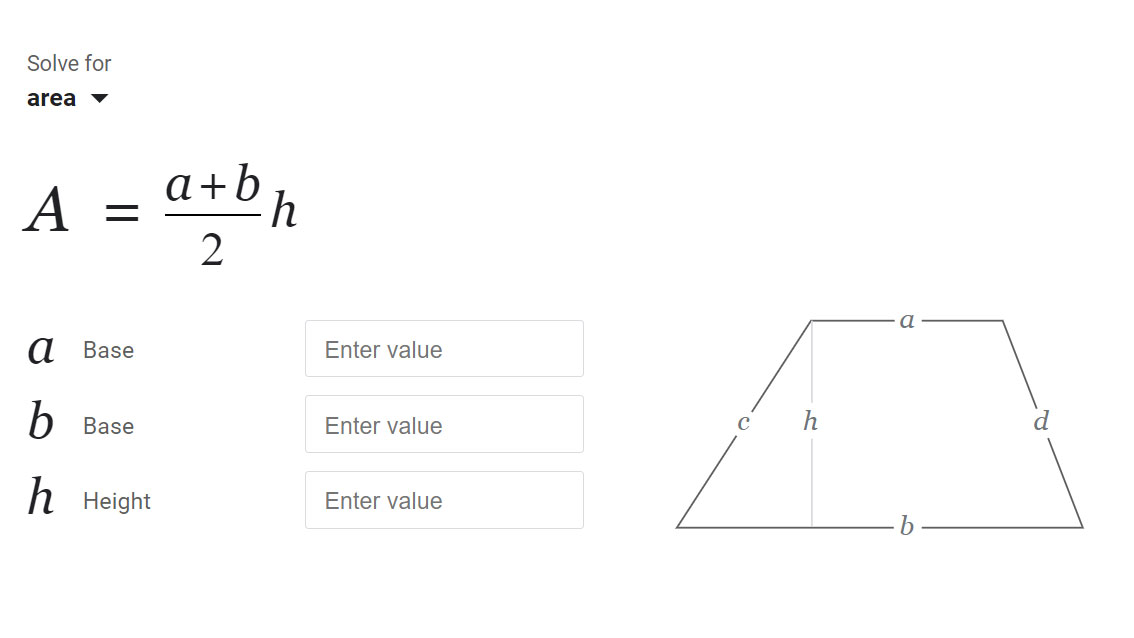
- Invoer: Bovenste basis a, onderste basis b, hoogte h (allemaal positieve reële getallen).
- Formule:
Oppervlakte = ((a + b) / 2) × h. Voor een beknopte referentie over de formule, zie Wolfram MathWorld: Trapezium. - Eenheden: De output is in vierkante eenheden. Als de invoer in meters is, is het resultaat in m²; als in inches, in in². Het hulpmiddel laat eenheden generiek om in elke context te passen.
- Visualisatie: Het diagram blijft altijd gecentreerd op het canvas en labelt dezelfde hoeveelheden die je hebt ingevoerd: a bovenaan, b onderaan, en h als de loodrechte afstand tussen hen.
- Numerieke stabiliteit: Het hulpmiddel accepteert decimalen, grote waarden en kleine waarden. Het rondt de weergave netjes af terwijl het interne precisie behoudt.
Waarom deze formule correct is
De oppervlakte van een trapezium is gelijk aan de hoogte vermenigvuldigd met het gemiddelde van de twee parallelle zijden. Intuïtief, als je de korte basis langs de hoogte “schuift”, kun je het trapezium herschikken in een rechthoek waarvan de breedte het gemiddelde van de twee bases is. Dat geeft A = h × (a + b)/2.
Stap-voor-stap voorbeelden
- Voorbeeld 1 (komt overeen met de standaardtekening):
- a = 6, b = 10, h = 4
- Gemiddelde van de bases = (6 + 10)/2 = 8
- Oppervlakte = 8 × 4 = 32 vierkante eenheden
- Voorbeeld 2 (decimalen):
- a = 3.5, b = 12, h = 2.8
- Gemiddelde van de bases = (3.5 + 12)/2 = 7.75
- Oppervlakte = 7.75 × 2.8 = 21.7 vierkante eenheden
- Voorbeeld 3 (smalle hoogte):
- a = 20, b = 24, h = 0.5
- Gemiddelde van de bases = 22
- Oppervlakte = 22 × 0.5 = 11 vierkante eenheden
Omgekeerde berekeningen die je misschien nodig hebt
- Los op voor hoogte gegeven oppervlakte en bases:
h = (2 × Oppervlakte) / (a + b) - Los op voor een onbekende basis gegeven oppervlakte, de andere basis en hoogte:
a = (2 × Oppervlakte) / h − b(of verwissel a en b)
Wat telt als de hoogte
Hoogte is loodrecht op de bases. Het is niet de schuine zijde. Als de zijden hellen, is de hoogte nog steeds de kortste rechte afstand tussen de twee bases. In rechthoekige of isosceles trapezia is dit gemakkelijk te zien; in obtuse gevallen blijft het loodrecht.
Kwaliteitscontroles en randgevallen
- Positiviteit: Alle drie de invoeren moeten groter zijn dan nul om een oppervlakte te produceren.
- Gelijke bases: Als a = b, wordt het trapezium een rechthoek; de formule reduceert tot
A = b × h, zoals verwacht. - Zeer grote of zeer kleine getallen: Oppervlakte schaalt lineair met hoogte en met het gemiddelde van de bases. Verdubbeling van elke invoer verdubbelt de oppervlakte voor hoogte en verdubbelt voor het gemiddelde van de bases zoals passend.
Reële trapeziumvormen
- Wegprofielen en medianen: Schouders en taluds vormen vaak trapezia wanneer ze van de zijkant worden bekeken.
- Dakconstructie: Sommige heup- of schuurdakpanelen, en gevelprofielen, zijn trapeziumvormig.
- Landschapsbedden en hellingen: Plattegrondweergaven en zijprofielen leveren vaak trapezia op.
- Blikonderdelen en tegels: Trapeziumvormige platen zijn gebruikelijk in de productie en vloeren.
- Greppels en kanalen: Technische doorsneden van sloten gebruiken vaak trapeziumvormige profielen.
Gebruik van het resultaat
- Materiaalinschatting: Vermenigvuldig de oppervlakte met de dikte om het volume te schatten (bijv. grond of beton). Houd de eenheidsconsistentie aan.
- Kostenraming: Als een materiaal per vierkante eenheid wordt geprijsd, vermenigvuldig dan de eenheidsprijs met jouw oppervlakte om de uitgaven te schatten.
- Schaaltekeningen: Als jouw invoeren afkomstig zijn van een geschaalde plattegrond, converteer dan naar reële eenheden voordat je de oppervlakte berekent.
Veelvoorkomende fouten om te vermijden
- Een schuine zijde gebruiken in plaats van de loodrechte hoogte.
- Eenheden onjuist toevoegen. Houd alle invoeren in dezelfde eenheid zodat de output in vierkante van die eenheid is.
- Vergeten dat de formule het gemiddelde van de bases gebruikt, niet hun verschil.
CalcuLife.com






Laat een reactie achter