Kalkulator for volum av avkortet pyramide

Denne nettbaserte kalkulatoren beregner volumet av en avkortet pyramide (frustum) for både kvadratiske og rektangulære baser. Den implementerer den standard frustum volumformelen med konsekvent enhetshåndtering og presisjonskontroll. Metoden er basert på klassisk geometri (se Frustum – Volum), så resultatene er matematisk pålitelige når inndataene er gyldige (ikke-negative dimensjoner med topp/bunn i samme enhet). Dette verktøyet er spesielt nyttig for norske brukere som ønsker å beregne volumet av strukturer i byggeteknikk og design.

Kalkulator for volum av avkuttet pyramide

Hva du vil oppgi

Bunnside a

Topp side b

Høyde h

Enhet

Desimaler

Volum

—

Oppsummering av inndata

Formel

V = (h / 3) · (A_bunn + A_topp + √(A_bunn · A_topp))
Kvadrat: A_bunn=a², A_topp=b² ⇒ V = (h/3)(a² + b² + ab)
Rektangulær: A_bunn=L₁·W₁, A_topp=L₂·W₂

Visualiseringen bruker en fast aksonometrisk projeksjon: topp- og bunnrektangler forblir parallelle og sentrerte; vertikale kanter skaleres med høyden din. Linjer markerer L (blå), B (grønn), og h (rød).

Dele dette?

Slik bruker du

Velg Kvadratisk, Rektangulær, eller Arealer modus.
Angi:
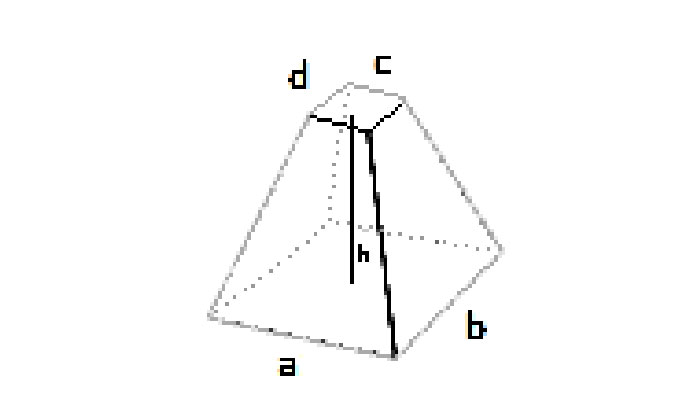
- Kvadratisk: bunnside a, toppside b, høyde h.
- Rektangulær: bunn L₁ × W₁, topp L₂ × W₂, høyde h.
- Arealer: bunnareal A_bottom, toppareal A_top, høyde h.
Velg enhet og desimalpresisjon, og klikk deretter Beregne.
Visualiseringen reflekterer dine proporsjoner: blå ≈ lengde (L), grønn ≈ bredde (W), rød ≈ høyde (h). Pillen nedenfor viser dine inndata for kopiering/innliming.

Formler

Generelt frustum volum

V = (h / 3) · (A_bottom + A_top + √(A_bottom · A_top))

Kvadratiske baser (bunnside a, toppside b):
A_bottom = a², A_top = b² ⇒ V = (h / 3) · (a² + b² + a·b)

Rektangulære baser (bunn L₁×W₁, topp L₂×W₂):
A_bottom = L₁·W₁, A_top = L₂·W₂ ⇒ V = (h / 3) · (L₁W₁ + L₂W₂ + √(L₁W₁·L₂W₂))

Sanitetskontroller. Hvis topp er lik bunn (A_top = A_bottom), blir formen et prisme og V = A_bottom·h. Hvis topp er 0, er det en full pyramide og V = (A_bottom·h)/3.

Forhåndsberegnede eksempler (alle inndata i cm; volum i cm³)

Modus	Bunn dimensjoner	Topp dimensjoner	h	Volum
Kvadratisk	a × a = 10 × 10	b × b = 6 × 6	12	784
Kvadratisk	a × a = 5 × 5	b × b = 5 × 5	8	200
Kvadratisk	a × a = 20 × 20	b × b = 10 × 10	15	3,500
Kvadratisk	a × a = 7.5 × 7.5	b × b = 3.2 × 3.2	18	542.94
Rektangulær	L₁×W₁ = 12 × 8	L₂×W₂ = 6 × 4	20	1,120
Rektangulær	L₁×W₁ = 50 × 40	L₂×W₂ = 30 × 20	35	43,113.5263
Rektangulær	L₁×W₁ = 15 × 10	L₂×W₂ = 15 × 5	12	1,324.2641

Alle verdier dobbeltsjekket med V = (h/3)(A_bottom + A_top + √(A_bottomA_top)). Avrunding vist til 2–4 desimaler der det er nyttig.

Praktiske tips & kvalitetskontroller

Hold enhetene konsistente. Angi alle lineære dimensjoner i samme enhet; kalkulatoren konverterer til volum i den enheten³ (f.eks. cm → cm³).
Mål høyden korrekt. Bruk den vinkelrette avstanden mellom basene (ikke en skrå kant).
Bruk Arealer-modus når du allerede vet bunnarealene (fra tegninger, CAD, eller målinger på stedet) for å unngå å forsterke avrundingsfeil.
Sanitetskontroll med ekstreme verdier: Hvis b → a, bør resultatet nærme seg A·h. Hvis b → 0, bør resultatet nærme seg (A·h)/3.
Presisjonskontroll: Øk “Desimaler” når inndataene er små eller når du planlegger å kjede beregninger (f.eks. til masse ved hjelp av tetthet).

CalcuLife.com