日常生活には、さまざまな円形の物体が存在します。例えば、コーヒーカップ、自転車のホイール、水道管、望遠鏡のレンズなどが挙げられます。建築、デザイン、工学、製造業などの分野では、円の周長(円周)を正確に計算する必要があることがよくあります。しかし、公式を覚えている必要はありません。このページでは、半径または直径を入力するだけで円周を計算できる便利なオンラインツールを提供しています。
円周計算ツール (半径または直径)
半径または直径を入力して円周を計算します。
半径 (R) または 直径 (D) を入力
計算結果 (円周 P)
計算プロセスがここに表示されます。
小数点以下の桁数
円周の計算方法
円周(P)を求めるには、次の2つの公式があります:
- P = 2πR (R は半径)
- P = πD (D は直径)
どちらの式でも、円周率 π(パイ)が使用されます。通常は 3.14 で計算しても十分ですが、より高精度な計算が必要な場合は 3.1415926535 を使用することも可能です。
円の基本概念
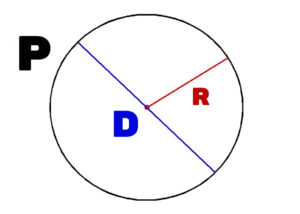
- 半径 (R):円の中心から円周までの距離。直径を2で割ることで求めることができます。
- 直径 (D):円の中心を通る線分の長さ。半径の2倍の値になります。
よく使われる円周の計算例
- 直径10cmの円の円周 ≈ 31.42cm
- 半径5mの円の円周 ≈ 31.42m
- 直径1.5mの円の円周 ≈ 4.71m
- 半径25cmのピザの円周 ≈ 157.08cm
- 直径100cmの大皿の円周 ≈ 314.16cm
- 半径0.35mの自転車ホイールの円周 ≈ 2.20m
- 直径20mのサーカスの円形ステージの円周 ≈ 62.83m
- 直径50mの円形競技場の円周 ≈ 157.08m
応用計算と追加情報
- 円の面積(A)を求める場合は、公式 A = πR² を使用します。
- 円の弧の長さ(L)を求めるには、中心角(θ)の度数を使って L = (θ / 360) × 2πR の公式を適用します。
- 円のセクター(扇形)の面積(S)は、S = (θ / 360) × πR² で計算できます。
- 円の内接・外接正多角形の計算も、円周を利用して求めることが可能です。
実生活での円周計算の用途
- 建築設計:円形の広場や噴水の設計
- 製造業:歯車やパイプの寸法決定
- デザイン:ロゴや円形オブジェクトの作成
- スポーツ:円形競技場やトラックの測定
- 料理:ピザやケーキのサイズ決定
- 天文学:惑星の軌道計算
© CalcuLife.com








コメントする