Le calculateur de surface d’un trapèze trouve la surface d’un trapèze à partir de ses deux bases et de sa hauteur en utilisant la formule géométrique standard. Les seules entrées dont vous avez besoin sont les longueurs de la base supérieure a, de la base inférieure b, et de la hauteur perpendiculaire h. La visualisation se centre et s’ajuste à vos chiffres afin que vous puissiez voir quel côté est lequel. Cet outil est particulièrement utile pour les étudiants et les professionnels en France qui travaillent avec des formes géométriques dans divers domaines.

Calculateur de surface du trapèze
h=0 a=0 b=0
Partager ceci ?
WhatsApp X Telegram Facebook LinkedIn Reddit

Comment fonctionne le calculateur

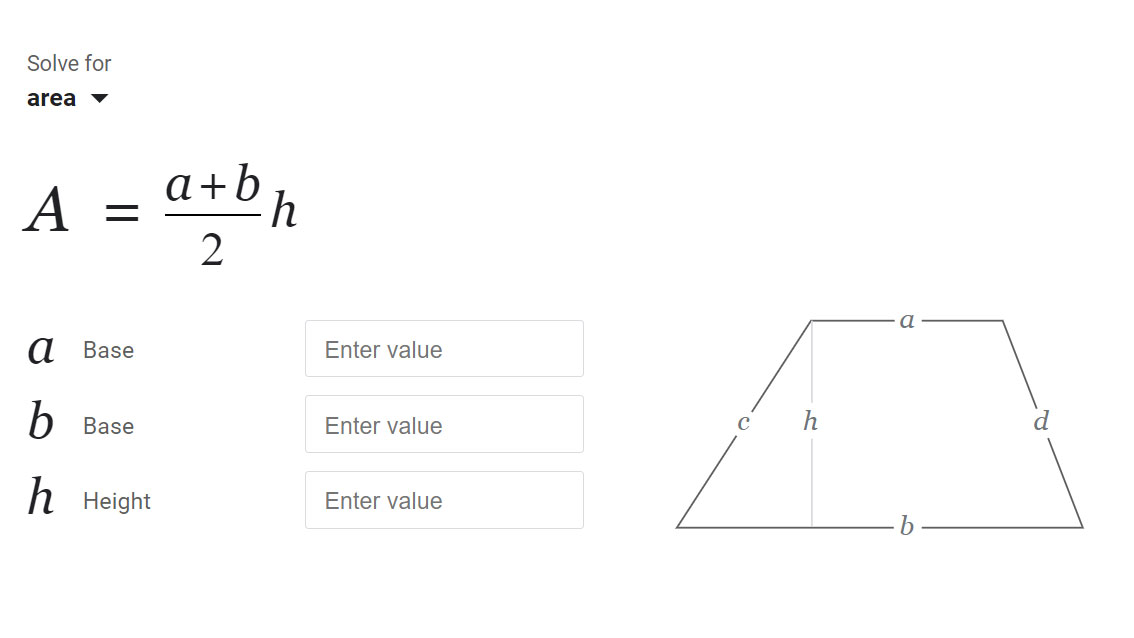
  • Entrées : Base supérieure a, base inférieure b, hauteur h (tous des nombres réels positifs).
  • Formule : Surface = ((a + b) / 2) × h. Pour une référence concise sur la formule, consultez Wolfram MathWorld : Trapèze.
  • Unités : La sortie est en unités carrées. Si les entrées sont en mètres, le résultat est en m² ; si en centimètres, en cm². L’outil laisse les unités génériques pour s’adapter à tout contexte.
  • Visualisation : Le diagramme reste toujours centré sur le canevas et étiquette les mêmes quantités que vous avez saisies : a en haut, b en bas, et h comme la distance perpendiculaire entre elles.
  • Stabilité numérique : L’outil accepte les décimales, les grandes valeurs et les petites valeurs. Il arrondit l’affichage de manière propre tout en maintenant une précision interne.

Pourquoi cette formule est correcte

La surface d’un trapèze est égale à la hauteur multipliée par la moyenne des deux côtés parallèles. Intuitivement, si vous “faites glisser” la base courte le long de la hauteur, vous pouvez réarranger le trapèze en un rectangle dont la largeur est la moyenne des deux bases. Cela donne A = h × (a + b)/2.

Calculateur de surface de trapèze avec visualisation

Exemples étape par étape

  1. Exemple 1 (correspond au dessin par défaut) :
    • a = 6, b = 10, h = 4
    • Moyenne des bases = (6 + 10)/2 = 8
    • Surface = 8 × 4 = 32 unités carrées
  2. Exemple 2 (décimales) :
    • a = 3,5, b = 12, h = 2,8
    • Moyenne des bases = (3,5 + 12)/2 = 7,75
    • Surface = 7,75 × 2,8 = 21,7 unités carrées
  3. Exemple 3 (hauteur fine) :
    • a = 20, b = 24, h = 0,5
    • Moyenne des bases = 22
    • Surface = 22 × 0,5 = 11 unités carrées

Calculs inverses dont vous pourriez avoir besoin

  • Résoudre pour la hauteur donnée la surface et les bases :
    h = (2 × Surface) / (a + b)
  • Résoudre pour une base inconnue donnée la surface, l’autre base et la hauteur :
    a = (2 × Surface) / h − b (ou échanger a et b)

Ce qui compte comme la hauteur

La hauteur est perpendiculaire aux bases. Ce n’est pas le côté incliné. Si les côtés penchent, la hauteur est toujours la distance droite la plus courte entre les deux bases. Dans les trapèzes rectangles ou isocèles, cela est facile à voir ; dans les cas obtus, cela reste perpendiculaire.

Contrôles de qualité et cas limites

  • Positivité : Les trois entrées doivent être supérieures à zéro pour produire une surface.
  • Bases égales : Si a = b, le trapèze devient un rectangle ; la formule se réduit à A = b × h, comme prévu.
  • Chiffres très grands ou très petits : La surface évolue linéairement avec la hauteur et avec la moyenne des bases. Doubler chaque entrée double la surface pour la hauteur et double pour la moyenne des bases, selon le cas.

Formes de trapèze dans le monde réel

  • Sections de route et terre-pleins : Les accotements et les talus forment souvent des trapèzes lorsqu’ils sont vus de côté.
  • Charpente de toit : Certains panneaux de toit à pignon ou à shed, et les profils de fascia, sont trapézoïdaux.
  • Massifs de jardin et rampes : Les vues de plan et les profils latéraux donnent fréquemment des trapèzes.
  • Pièces en tôle et carreaux : Les découpes trapézoïdales sont courantes dans la fabrication et les aménagements de sol.
  • Tranchées et canaux : Les sections transversales d’ingénierie des fossés utilisent souvent des profils trapézoïdaux.

Utilisation du résultat

  • Estimation des matériaux : Multipliez la surface par l’épaisseur pour approximer le volume (par exemple, sol ou béton). Gardez la cohérence des unités.
  • Coût : Si un matériau est tarifé par unité carrée, multipliez le coût unitaire par votre surface pour estimer les dépenses.
  • Échelle des dessins : Si vos entrées proviennent d’un plan à l’échelle, convertissez en unités réelles avant de calculer la surface.

Erreurs courantes à éviter

  • Utiliser un côté incliné au lieu de la hauteur perpendiculaire.
  • Ajouter des unités incorrectement. Gardez toutes les entrées dans la même unité afin que la sortie soit en carré de cette unité.
  • Oublier que la formule utilise la moyenne des bases, et non leur différence.

CalcuLife.com