Calculateur de volume de pyramide tronquée

Ce calculateur en ligne calcule le volume d’un cône tronqué (frustum) pour des bases carrées et rectangulaires. Il applique la formule standard du volume du frustum avec une gestion cohérente des unités et un contrôle de la précision. La méthode est basée sur la géométrie classique (voir Frustum – Volume), donc les résultats sont mathématiquement fiables lorsque les entrées sont valides (dimensions non négatives avec le haut/la base dans la même unité). Cet outil est particulièrement utile pour les architectes et les ingénieurs en France qui travaillent sur des projets nécessitant des calculs de volume précis.

Calculateur de Volume de Pyramide Truncée

Ce que vous allez entrer

Côté inférieur a

Côté supérieur b

Hauteur h

Unité

Décimales

Volume

—

Récapitulatif des Entrées

Formule

V = (h / 3) · (A_base + A_haut + √(A_base · A_haut))
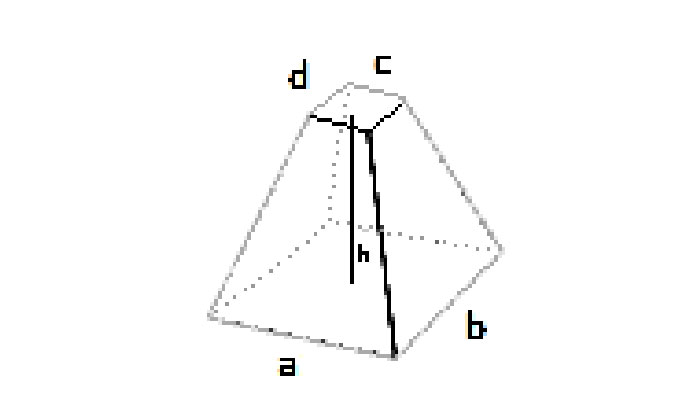
Carré : A_base=a², A_haut=b² ⇒ V = (h/3)(a² + b² + ab)
Rectangulaire : A_base=L₁·l₁, A_haut=L₂·l₂

La visualisation utilise une projection axonométrique fixe : les rectangles supérieur et inférieur restent parallèles et centrés ; les arêtes verticales s'échelonnent avec votre hauteur. Les guides marquent L (bleu), l (vert), et h (rouge).

Partager ceci ?

Comment utiliser

Choisissez le mode Carré, Rectangulaire ou Surfaces.
Entrez :
- Carré : côté inférieur a, côté supérieur b, hauteur h.
- Rectangulaire : inférieur L₁ × W₁, supérieur L₂ × W₂, hauteur h.
- Surfaces : surface inférieure A_bottom, surface supérieure A_top, hauteur h.
Sélectionnez l’unité et la précision décimale, puis cliquez sur Calculer.
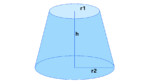
La visualisation reflète vos proportions : bleu ≈ longueur (L), vert ≈ largeur (W), rouge ≈ hauteur (h). La pilule ci-dessous montre vos entrées pour copier/coller.

Formules

Volume général du frustum

V = (h / 3) · (A_bottom + A_top + √(A_bottom · A_top))

Bases carrées (côté inférieur a, côté supérieur b) :
A_bottom = a², A_top = b² ⇒ V = (h / 3) · (a² + b² + a·b)

Bases rectangulaires (inférieur L₁×W₁, supérieur L₂×W₂) :
A_bottom = L₁·W₁, A_top = L₂·W₂ ⇒ V = (h / 3) · (L₁W₁ + L₂W₂ + √(L₁W₁·L₂W₂))

Vérifications de cohérence. Si le haut est égal au bas (A_top = A_bottom), la forme devient un prisme et V = A_bottom·h. Si le haut est 0, c’est un cône plein et V = (A_bottom·h)/3.

Exemples pré-calculés (toutes les entrées en cm ; volumes en cm³)

Mode	Dimensions inférieures	Dimensions supérieures	h	Volume
Carré	a × a = 10 × 10	b × b = 6 × 6	12	784
Carré	a × a = 5 × 5	b × b = 5 × 5	8	200
Carré	a × a = 20 × 20	b × b = 10 × 10	15	3,500
Carré	a × a = 7.5 × 7.5	b × b = 3.2 × 3.2	18	542.94
Rectangulaire	L₁×W₁ = 12 × 8	L₂×W₂ = 6 × 4	20	1,120
Rectangulaire	L₁×W₁ = 50 × 40	L₂×W₂ = 30 × 20	35	43,113.5263
Rectangulaire	L₁×W₁ = 15 × 10	L₂×W₂ = 15 × 5	12	1,324.2641

Toutes les valeurs vérifiées avec V = (h/3)(A_bottom + A_top + √(A_bottomA_top)). Arrondi affiché à 2–4 décimales lorsque cela est utile.

Conseils pratiques & Vérifications de qualité

Gardez les unités cohérentes. Entrez toutes les dimensions linéaires dans la même unité ; le calculateur convertit en volume dans cette unité³ (par exemple, cm → cm³).
Mesurez correctement la hauteur. Utilisez la distance perpendiculaire entre les bases (pas un bord incliné).
Utilisez le mode Surfaces lorsque vous connaissez déjà les surfaces de base (à partir de dessins, CAD ou mesures sur site) pour éviter d’accumuler des erreurs d’arrondi.
Vérifiez la cohérence avec des extrêmes : Si b → a, le résultat doit approcher A·h. Si b → 0, le résultat doit approcher (A·h)/3.
Contrôle de précision : Augmentez les “Décimales” lorsque les entrées sont petites ou lorsque vous prévoyez de chaîner des calculs (par exemple, pour la masse en utilisant la densité).

CalcuLife.com