Kalkulátor plochy lichoběžníku s vizualizací

Kalkulačka plochy trapezoidu najde plochu trapezoidu z jeho dvou základů a výšky pomocí standardního geometrického vzorce. Jediné vstupy, které potřebujete, jsou délky horní základny a, dolní základny b a kolmé výšky h. Vizualizace se zaměřuje a škáluje na vaše čísla, takže můžete vidět, která strana je která. Tento nástroj je obzvlášť užitečný pro studenty a profesionály v České republice, kteří se zabývají geometrií a stavebnictvím.

Sdílet tohle?

Kopírovat odkaz ✓

Jak kalkulačka funguje

• Vstupy: Horní základna a, dolní základna b, výška h (všechny kladná reálná čísla).
• Vzorec: Plocha = ((a + b) / 2) × h. Pro stručnou referenci k vzorci viz Wolfram MathWorld: Trapezoid.
• Jednotky: Výstup je v čtverečních jednotkách. Pokud jsou vstupy v metrech, výsledek je v m²; pokud v palcích, v in². Nástroj ponechává jednotky obecné, aby vyhovovaly jakémukoli kontextu.
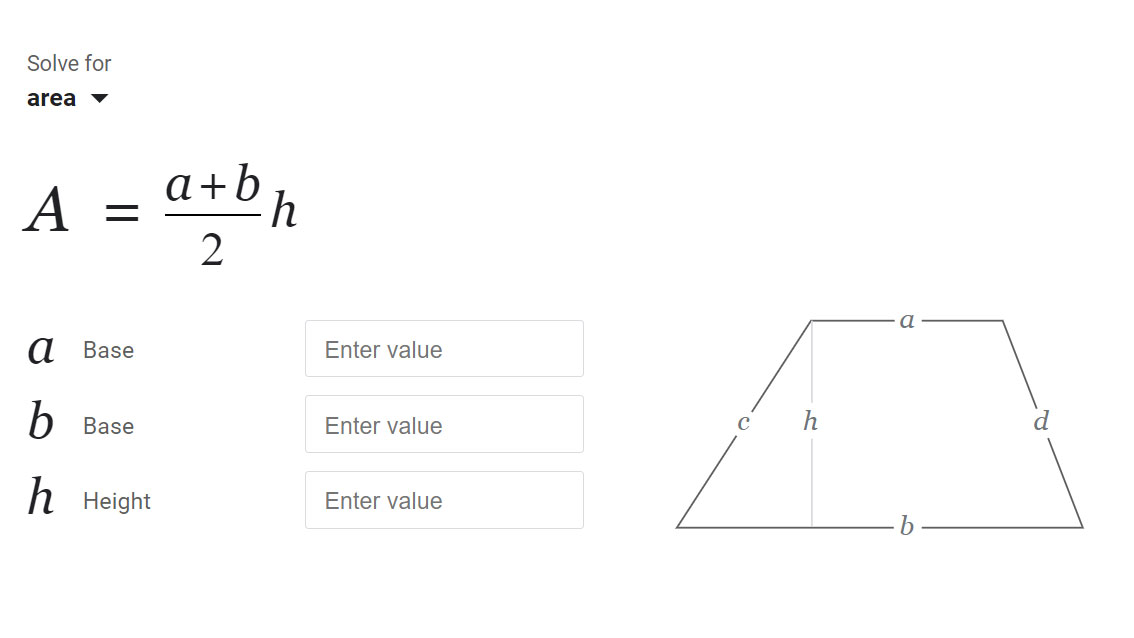
• Vizualizace: Diagram zůstává vždy vycentrovaný na plátně a označuje stejné množství, které jste zadali: a nahoře, b dole a h jako kolmá vzdálenost mezi nimi.
• Číselná stabilita: Nástroj přijímá desetinná čísla, velké hodnoty a malé hodnoty. Zaokrouhluje zobrazení čistě, zatímco zachovává vnitřní přesnost.

Proč je tento vzorec správný

Plocha trapezoidu se rovná výšce krát průměr dvou rovnoběžných stran. Intuitivně, pokud „posunete“ krátkou základnu podél výšky, můžete uspořádat trapezoid do obdélníku, jehož šířka je průměr dvou základů. To dává P = h × (a + b)/2.

Příklady krok za krokem

1. Příklad 1 (odpovídá výchozímu výkresu):
   • a = 6, b = 10, h = 4
   • Průměr základů = (6 + 10)/2 = 8
   • Plocha = 8 × 4 = 32 čtverečních jednotek
2. Příklad 2 (desetinná čísla):
   • a = 3.5, b = 12, h = 2.8
   • Průměr základů = (3.5 + 12)/2 = 7.75
   • Plocha = 7.75 × 2.8 = 21.7 čtverečních jednotek
3. Příklad 3 (úzká výška):
   • a = 20, b = 24, h = 0.5
   • Průměr základů = 22
   • Plocha = 22 × 0.5 = 11 čtverečních jednotek

Obrácené výpočty, které můžete potřebovat

• Vyřešit pro výšku danou plochou a základy:
  h = (2 × Plocha) / (a + b)
• Vyřešit pro neznámou základnu danou plochou, druhou základnou a výškou:
  a = (2 × Plocha) / h − b (nebo prohoďte a a b)

Co se počítá jako výška

Výška je kolmá na základy. Není to šikmá strana. Pokud jsou strany nakloněné, výška je stále nejkratší přímá vzdálenost mezi dvěma základy. U pravých nebo isosceles trapezoidů je to snadné vidět; v obtusních případech zůstává kolmá.

Kvalitativní kontroly a okrajové případy

• Kladnost: Všechny tři vstupy musí být větší než nula, aby se vytvořila plocha.
• Rovné základy: Pokud a = b, trapezoid se stává obdélníkem; vzorec se zjednoduší na P = b × h, jak se očekává.
• Velmi velká nebo velmi malá čísla: Plocha se lineárně mění s výškou a s průměrem základů. Dvojnásobení každého vstupu zdvojnásobí plochu pro výšku a zdvojnásobí průměr základů podle potřeby.

Skutečné tvary trapezoidů

• Průřezy silnic a středové pruhy: Ramena a násypy často tvoří trapezoidy, když jsou viděny z boku.
• Konstrukce střech: Některé panely s hip nebo pultovou střechou a profily okapů jsou trapezoidální.
• Záhony a rampy: Plánové pohledy a boční profily často vytvářejí trapezoidy.
• Součásti z plechu a dlaždice: Trapezoidní výlisky jsou běžné ve výrobě a rozvržení podlah.
• Příkopy a kanály: Inženýrské průřezy příkopů často používají trapezoidní profily.

Použití výsledku

• Odhad materiálů: Vynásobte plochu tloušťkou pro přibližný objem (např. půda nebo beton). Udržujte jednotkovou konzistenci.
• Odhad nákladů: Pokud je materiál oceněn na čtvereční jednotku, vynásobte jednotkovou cenu vaší plochou pro odhad výdajů.
• Škálování výkresů: Pokud vaše vstupy pocházely z měřítkového plánu, převedete na reálné jednotky před výpočtem plochy.

Časté chyby, kterým se vyhnout

• Použití šikmé strany místo kolmé výšky.
• Nesprávné přidávání jednotek. Udržujte všechny vstupy ve stejné jednotce, aby výstup byl ve čtverci této jednotky.
• Zapomínání, že vzorec používá průměr základů, nikoli jejich rozdíl.

CalcuLife.com