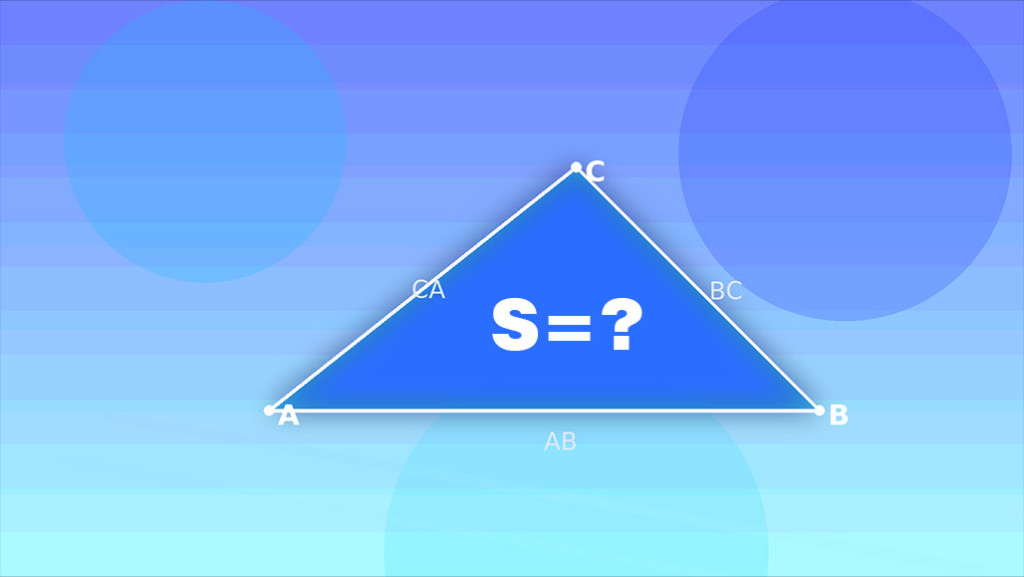
حاسبة عبر الإنترنت لمساحة مثلث من ثلاثة أطوال جوانب (AB، BC، CA) باستخدام صيغة هيرون. تتحقق من عدم المساواة في المثلث، وتظهر رسمًا بيانيًا نسبيًا مع الرؤوس A وB وC، وترسم “محاولة السقف” بوضوح لمجموعات غير ممكنة. يحتفظ الرسم البياني بأطوال الجوانب في نسبة بصرية صحيحة. تظهر التسميات على الحواف (AB، BC، CA) وعلى الرؤوس (A، B، C).
حاسبة مساحة المثلث (3 أضلاع)
أدخل أطوال الأضلاع AB، BC، CA. يتم حساب المساحة (S) باستخدام صيغة هيرون. يحتفظ الرسم التوضيحي بالنسب الحقيقية ويضع علامات A وB وC والأضلاع AB وBC وCA. إذا لم تتمكن الأضلاع من تشكيل مثلث، يتم رسم "محاولة سقف" واضحة مع الفجوة ويظهر الناتج "غير موجود".
الضلع AB
الضلع BC
الضلع CA
المساحة (S)
كيفية الاستخدام
- أدخل ثلاثة أطوال جوانب موجبة لـ AB وBC وCA.
- اضغط على احسب.
- اقرأ المساحة S واستعرض العمل والرسم البياني.
- استخدم الأماكن العشرية للتحكم في تقريب النتيجة والتسميات.
ملاحظات: إذا لم تتمكن الجوانب من تشكيل مثلث، تظهر النتيجة “غير موجودة” والرؤية البيانية ترسم الجانب الأطول كقاعدة مع ذراعين متقطعين لا يلتقيان، مما يبرز الفجوة.
استخدم وحدات متسقة لجميع الجوانب؛ ستكون المساحة بتلك الوحدات مربعة (م²، سم²، بوصة²، قدم²، إلخ).
الصيغ
عدم المساواة في المثلث (الوجود): AB + BC > CA، AB + CA > BC، BC + CA > AB (جميعها صارمة).
نصف المحيط: s = (AB + BC + CA) / 2
صيغة هيرون (المساحة): S = √[ s(s − AB)(s − BC)(s − CA) ]
- شكل مكافئ: S = (1/4) √[(AB + BC + CA)(−AB + BC + CA)(AB − BC + CA)(AB + BC − CA)].
- من المساحة إلى الارتفاع على AB: hAB = 2S / AB (بالمثل بالنسبة للقواعد الأخرى).
- مع نصف القطر الداخلي r ونصف القطر الخارجي R: S = r·s = (AB·BC·CA)/(4R).
- مثلث متساوي الأضلاع (الجانب a): S = (√3/4)·a².
قيم أمثلة
| AB | BC | CA | صالح؟ | المساحة S |
| 3 | 4 | 5 | نعم | 6 |
| 5 | 5 | 6 | نعم | 12 |
| 7 | 5 | 6 | نعم | 14.6969 |
| 8 | 8 | 8 | نعم | 27.7128 |
| 10 | 6 | 8 | نعم | 24 |
| 9 | 12 | 15 | نعم | 54 |
| 2.5 | 4 | 5 | نعم | 4.9525 |
| 12 | 13 | 5 | نعم | 30 |
| 20 | 13 | 7 | لا | — |
| 6.5 | 6.5 | 4.2 | نعم | 12.918 |
| 15 | 14 | 9 | نعم | 61.6441 |
| 30 | 29 | 10 | نعم | 144.6373 |
| 100 | 120 | 150 | نعم | 5981.168 |
| 1.2 | 1.3 | 2.4 | نعم | 0.4196 |
| 9 | 9 | 18 | لا | — |
حقائق مثيرة للاهتمام
- نتيجة هيرون: تُنسب الصيغة إلى هيرون الإسكندري (القرن الأول الميلادي) وتحتاج فقط إلى أطوال الجوانب، دون الحاجة إلى زوايا أو ارتفاعات.
- مثلثات هيرونية: المثلثات ذات الجوانب الصحيحة والمساحة الصحيحة (مثل 3-4-5 لها S = 6) تُسمى مثلثات هيرونية.
- أقصى مساحة: بالنسبة لمحيط ثابت، فإن المثلث المتساوي الأضلاع له أكبر مساحة. بالنسبة لقاعدتين ثابتتين، تكون المساحة في أقصى حد عندما تكون الزاوية المضمنة 90°.
- الانحلال: عندما يساوي مجموع واحد الجانب الثالث (مثل 20، 13، 7)، ينهار “المثلث” إلى قطعة ويكون S = 0.
- التحقق: من S وقاعدة، يمكن استعادة الارتفاعات، ونصف القطر الداخلي (r = S/s)، ونصف القطر الخارجي (R = AB·BC·CA/(4S)) مباشرة.
CalcuLife.com







اترك تعليقًا