حاسبة مساحة شبه المنحرف مع التصور

حاسبة مساحة شبه المنحرف تجد مساحة شبه المنحرف من قاعدتيه وارتفاعه باستخدام الصيغة الهندسية القياسية. المدخلات الوحيدة التي تحتاجها هي أطوال القاعدة العليا a، والقاعدة السفلية b، والارتفاع العمودي h. يتمركز العرض المرئي ويتناسب مع أرقامك حتى تتمكن من رؤية أي جانب هو أي. هذه الأداة مفيدة بشكل خاص للطلاب والمعلمين في الدول العربية حيث تساهم في فهم الهندسة بشكل أفضل.

هل تريد مشاركة هذا؟

نسخ الرابط ✓

كيف تعمل الحاسبة

• المدخلات: القاعدة العليا a، القاعدة السفلية b، الارتفاع h (جميعها أعداد حقيقية موجبة).
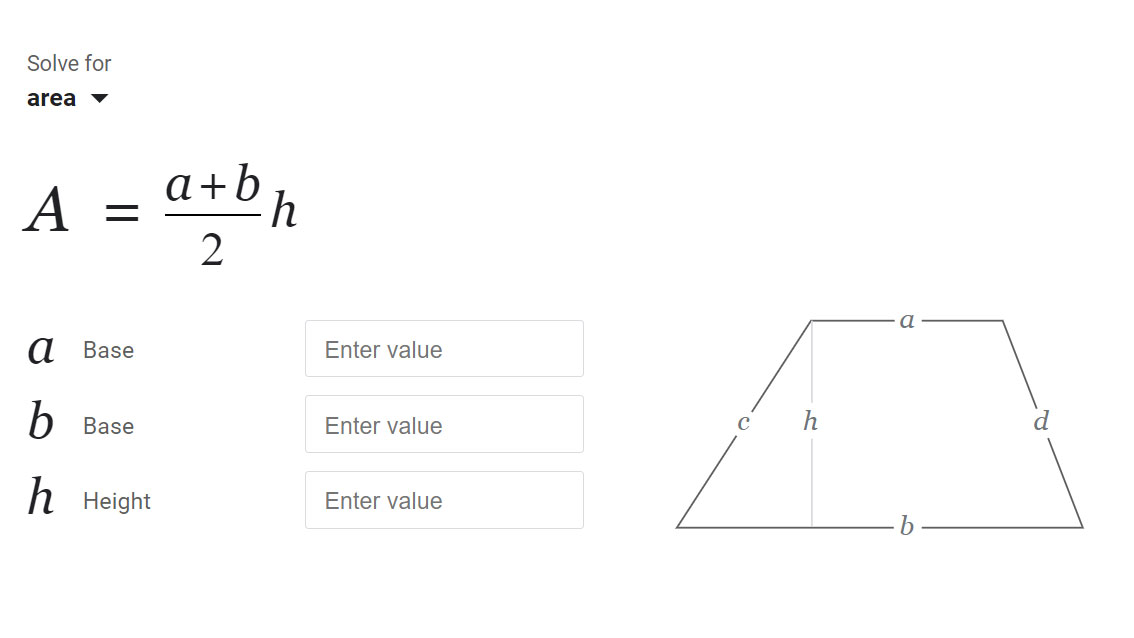
• الصيغة: المساحة = ((a + b) / 2) × h. لمراجعة مختصرة حول الصيغة، انظر Wolfram MathWorld: شبه المنحرف.
• الوحدات: الناتج يكون بوحدات مربعة. إذا كانت المدخلات بالمتر، فإن النتيجة تكون بالمتر المربع؛ إذا كانت بالبوصة، فإنها تكون بالبوصة المربعة. تترك الأداة الوحدات عامة لتناسب أي سياق.
• التصور: يبقى الرسم البياني دائمًا مركزيًا في اللوحة ويضع علامات على نفس الكميات التي كتبتها: a عبر الأعلى، b عبر الأسفل، وh كالمسافة العمودية بينهما.
• الاستقرار العددي: تقبل الأداة الأعداد العشرية، والقيم الكبيرة، والقيم الصغيرة. تقوم بتقريب العرض بشكل نظيف مع الحفاظ على الدقة الداخلية.

لماذا هذه الصيغة صحيحة

تساوي مساحة شبه المنحرف الارتفاع مضروبًا في المتوسط للجانبين المتوازيين. بشكل بديهي، إذا قمت بـ “تحريك” القاعدة القصيرة على طول الارتفاع، يمكنك إعادة ترتيب شبه المنحرف إلى مستطيل عرضُه هو متوسط القاعدتين. وهذا يعطي A = h × (a + b)/2.

أمثلة خطوة بخطوة

1. مثال 1 (يتطابق مع الرسم الافتراضي):
   • a = 6، b = 10، h = 4
   • متوسط القاعدتين = (6 + 10)/2 = 8
   • المساحة = 8 × 4 = 32 وحدة مربعة
2. مثال 2 (أعداد عشرية):
   • a = 3.5، b = 12، h = 2.8
   • متوسط القاعدتين = (3.5 + 12)/2 = 7.75
   • المساحة = 7.75 × 2.8 = 21.7 وحدة مربعة
3. مثال 3 (ارتفاع نحيف):
   • a = 20، b = 24، h = 0.5
   • متوسط القاعدتين = 22
   • المساحة = 22 × 0.5 = 11 وحدة مربعة

حسابات عكسية قد تحتاجها

• احسب الارتفاع المعطى المساحة والقاعدتين:
  h = (2 × المساحة) / (a + b)
• احسب قاعدة غير معروفة معطاة المساحة، والقاعدة الأخرى، والارتفاع:
  a = (2 × المساحة) / h − b (أو قم بتبديل a وb)

ما الذي يُعتبر ارتفاعًا

الارتفاع عمودي على القاعدتين. ليس الجانب المائل. إذا كانت الجوانب مائلة، فإن الارتفاع لا يزال هو أقصر مسافة مستقيمة بين القاعدتين. في شبه المنحرف القائم أو المتساوي الساقين، من السهل رؤية ذلك؛ في الحالات المنفرجة يبقى عموديًا.

فحوصات الجودة والحالات الحدية

• الإيجابية: يجب أن تكون جميع المدخلات الثلاثة أكبر من الصفر لإنتاج مساحة.
• القاعدتان المتساويتان: إذا كان a = b، يصبح شبه المنحرف مستطيلًا؛ وتقل الصيغة إلى A = b × h، كما هو متوقع.
• أعداد كبيرة جدًا أو صغيرة جدًا: تتناسب المساحة خطيًا مع الارتفاع ومع متوسط القاعدتين. مضاعفة كل مدخل تضاعف المساحة بالنسبة للارتفاع وتضاعف لمتوسط القاعدتين كما هو مناسب.

أشكال شبه المنحرف في العالم الحقيقي

• مقاطع الطرق والوسائط: غالبًا ما تشكل الأكتاف والمرتفعات أشكال شبه منحرف عند رؤيتها من الجانب.
• إطارات الأسطح: بعض الألواح ذات السقف المائل أو السقف المائل، وملفات الحواف، تكون شبه منحرف.
• أسرة المناظر الطبيعية والممرات: غالبًا ما تعطي الخطط الجانبية والملفات الجانبية أشكال شبه منحرف.
• قطع المعادن والألواح: الألواح شبه المنحرفة شائعة في التصنيع وتخطيطات الأرضيات.
• الخنادق والقنوات: غالبًا ما تستخدم مقاطع الهندسة للخنادق أشكال شبه منحرف.

استخدام النتيجة

• تقدير المواد: اضرب المساحة في السماكة لتقريب الحجم (مثل، التربة أو الخرسانة). حافظ على اتساق الوحدات.
• التكلفة: إذا كانت المادة مُسعّرة لكل وحدة مربعة، اضرب تكلفة الوحدة في المساحة الخاصة بك لتقدير الإنفاق.
• توسيع الرسومات: إذا كانت مدخلاتك جاءت من خطة مقاسة، قم بتحويلها إلى وحدات العالم الحقيقي قبل حساب المساحة.

أخطاء شائعة يجب تجنبها

• استخدام جانب مائل بدلاً من الارتفاع العمودي.
• إضافة الوحدات بشكل غير صحيح. حافظ على جميع المدخلات في نفس الوحدة بحيث يكون الناتج في مربع تلك الوحدة.
• نسيان أن الصيغة تستخدم متوسط القاعدتين، وليس الفرق بينهما.

CalcuLife.com