Máy tính diện tích hình thang tìm diện tích của một hình thang từ hai đáy và chiều cao của nó bằng cách sử dụng công thức hình học tiêu chuẩn. Các đầu vào bạn cần chỉ là độ dài của đáy trên a, đáy dưới b, và chiều cao vuông góc h. Hình ảnh trực quan sẽ tập trung và điều chỉnh theo các số của bạn để bạn có thể thấy bên nào là bên nào. Công cụ này rất hữu ích cho những ai cần tính toán diện tích hình thang trong các lĩnh vực như xây dựng và kiến trúc tại Việt Nam.
Cách máy tính hoạt động
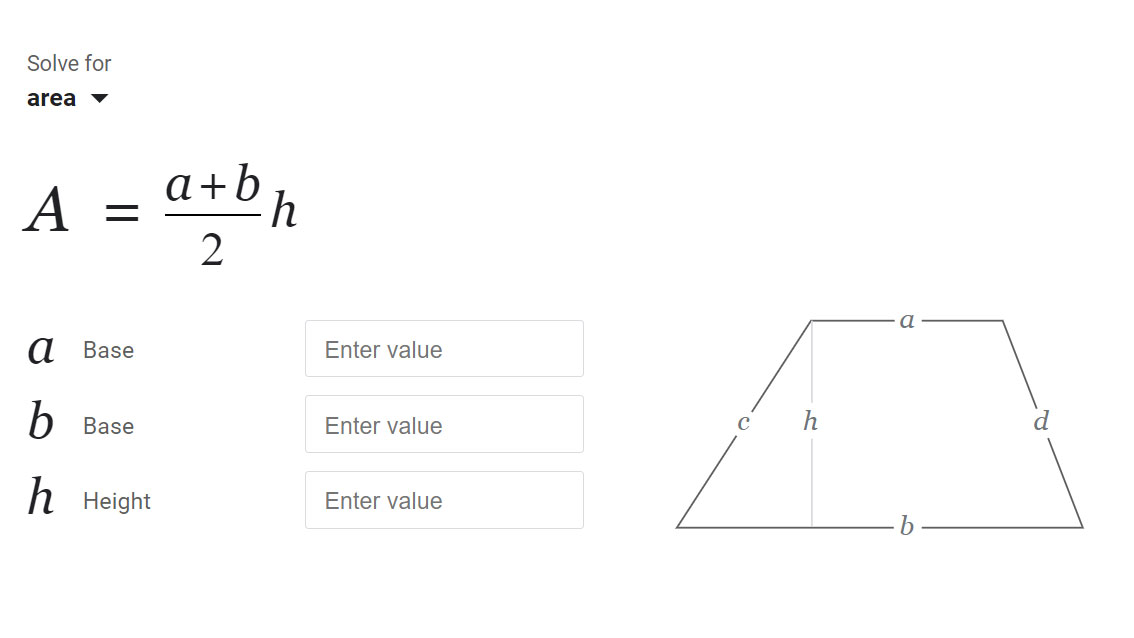
- Đầu vào: Đáy trên a, đáy dưới b, chiều cao h (tất cả là số thực dương).
- Công thức:
Diện tích = ((a + b) / 2) × h. Để tham khảo ngắn gọn về công thức, xem Wolfram MathWorld: Hình thang. - Đơn vị: Kết quả là đơn vị diện tích. Nếu đầu vào là mét, kết quả là m²; nếu là inch, là in². Công cụ để đơn vị chung để phù hợp với bất kỳ ngữ cảnh nào.
- Trực quan hóa: Sơ đồ luôn giữ vị trí trung tâm trên canvas và gán nhãn cho các đại lượng giống như bạn đã nhập: a ở trên cùng, b ở dưới cùng, và h là khoảng cách vuông góc giữa chúng.
- Độ ổn định số: Công cụ chấp nhận số thập phân, giá trị lớn và giá trị nhỏ. Nó làm tròn hiển thị một cách sạch sẽ trong khi vẫn giữ độ chính xác bên trong.
Tại sao công thức này là chính xác
Diện tích của một hình thang bằng chiều cao nhân với trung bình của hai cạnh song song. Một cách trực quan, nếu bạn “trượt” đáy ngắn dọc theo chiều cao, bạn có thể sắp xếp lại hình thang thành một hình chữ nhật có chiều rộng là trung bình của hai đáy. Điều đó cho A = h × (a + b)/2.
Ví dụ từng bước
- Ví dụ 1 (khớp với bản vẽ mặc định):
- a = 6, b = 10, h = 4
- Trung bình của các đáy = (6 + 10)/2 = 8
- Diện tích = 8 × 4 = 32 đơn vị diện tích
- Ví dụ 2 (số thập phân):
- a = 3.5, b = 12, h = 2.8
- Trung bình của các đáy = (3.5 + 12)/2 = 7.75
- Diện tích = 7.75 × 2.8 = 21.7 đơn vị diện tích
- Ví dụ 3 (chiều cao mỏng):
- a = 20, b = 24, h = 0.5
- Trung bình của các đáy = 22
- Diện tích = 22 × 0.5 = 11 đơn vị diện tích
Các phép tính ngược bạn có thể cần
- Tìm chiều cao cho diện tích và các đáy:
h = (2 × Diện tích) / (a + b) - Tìm một đáy chưa biết cho diện tích, đáy còn lại và chiều cao:
a = (2 × Diện tích) / h − b(hoặc hoán đổi a và b)
Chiều cao được tính như thế nào
Chiều cao vuông góc với các đáy. Nó không phải là cạnh nghiêng. Nếu các cạnh nghiêng, chiều cao vẫn là khoảng cách thẳng ngắn nhất giữa hai đáy. Trong các hình thang vuông hoặc cân, điều này dễ dàng nhận thấy; trong các trường hợp tùy ý, nó vẫn giữ tính vuông góc.
Kiểm tra chất lượng và các trường hợp đặc biệt
- Tính dương: Tất cả ba đầu vào phải lớn hơn không để tạo ra một diện tích.
- Các đáy bằng nhau: Nếu a = b, hình thang trở thành một hình chữ nhật; công thức giảm thành
A = b × h, như mong đợi. - Số rất lớn hoặc rất nhỏ: Diện tích tỷ lệ thuận với chiều cao và với trung bình của các đáy. Nhân đôi mọi đầu vào sẽ nhân đôi diện tích cho chiều cao và nhân đôi cho trung bình của các đáy như thích hợp.
Hình dạng hình thang trong thực tế
- Các mặt cắt ngang của đường và dải phân cách: Các bờ và đê thường tạo thành hình thang khi nhìn từ bên cạnh.
- Kết cấu mái: Một số tấm mái hình chóp hoặc mái hiên, và các hồ sơ bờ mái, có hình dạng hình thang.
- Các bồn cảnh quan và ramp: Các mặt bằng và hồ sơ bên thường tạo ra hình thang.
- Các bộ phận kim loại tấm và gạch: Các tấm hình thang là phổ biến trong sản xuất và bố trí sàn.
- Hố và kênh: Các mặt cắt kỹ thuật của rãnh thường sử dụng hồ sơ hình thang.
Sử dụng kết quả
- Ước lượng vật liệu: Nhân diện tích với độ dày để ước tính thể tích (ví dụ: đất hoặc bê tông). Giữ tính nhất quán về đơn vị.
- Tính toán chi phí: Nếu một vật liệu được định giá theo đơn vị diện tích, nhân chi phí đơn vị với diện tích của bạn để ước tính chi tiêu.
- Tỷ lệ bản vẽ: Nếu đầu vào của bạn đến từ một kế hoạch tỷ lệ, hãy chuyển đổi sang đơn vị thực tế trước khi tính toán diện tích.
Các lỗi thường gặp cần tránh
- Sử dụng một cạnh nghiêng thay vì chiều cao vuông góc.
- Thêm đơn vị không chính xác. Giữ tất cả các đầu vào trong cùng một đơn vị để đầu ra là diện tích của đơn vị đó.
- Quên rằng công thức sử dụng trung bình của các đáy, không phải sự khác biệt của chúng.
CalcuLife.com







Để lại bình luận