Volymberäknare för avskuren pyramid

Denna online-kalkylator beräknar volymen av en avskuren pyramid (frustum) för både kvadratiska och rektangulära baser. Den implementerar den standardiserade formeln för frustumvolym med konsekvent enhetshantering och precision. Metoden baseras på klassisk geometri (se Frustum – Volym), så resultaten är matematiskt tillförlitliga när indata är giltiga (icke-negativa dimensioner med topp/bas i samma enhet). Detta verktyg är särskilt användbart för svenska användare som arbetar med byggprojekt eller design där exakta volymberäkningar är avgörande.

Beräknare för volym av avskuren pyramid

Vad du kommer att ange

Botten sida a

Toppen sida b

Höjd h

Enhet

Decimaler

Volym

—

Sammanfattning av indata

Formel

V = (h / 3) · (A_botten + A_toppen + √(A_botten · A_toppen))
Kvadrat: A_botten=a², A_toppen=b² ⇒ V = (h/3)(a² + b² + ab)
Rektangulär: A_botten=L₁·W₁, A_toppen=L₂·W₂

Visualiseringen använder en fast axonometrisk projektion: topp- och bottenrektanglar förblir parallella och centrerade; vertikala kanter skalas med din höjd. Guider markerar L (blå), W (grön) och h (röd).

Dela det här?

Så här använder du

Välj Kvadratisk, Rektangulär eller Ytor läge.
Ange:
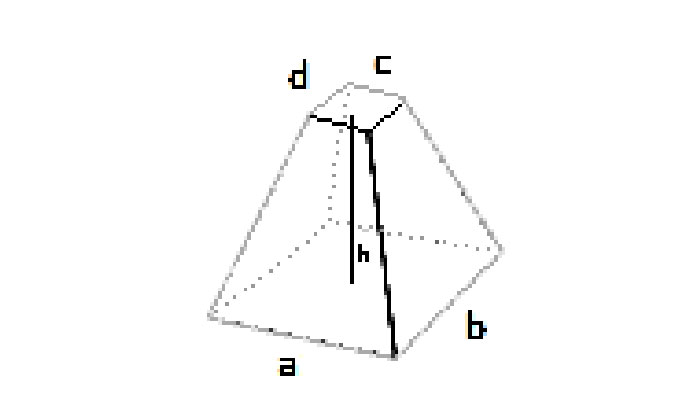
- Kvadratisk: botten sida a, topp sida b, höjd h.
- Rektangulär: botten L₁ × W₁, topp L₂ × W₂, höjd h.
- Ytor: bottenyta A_botten, toppyta A_top, höjd h.
Välj enhet och decimalprecision, klicka sedan på Beräkna.
Visualiseringen återspeglar dina proportioner: blå ≈ längd (L), grön ≈ bredd (W), röd ≈ höjd (h). Pillen nedan visar dina indata för kopiering/klippning.

Formler

Allmän frustumvolym

V = (h / 3) · (A_botten + A_top + √(A_botten · A_top))

Kvadratiska baser (botten sida a, topp sida b):
A_botten = a², A_top = b² ⇒ V = (h / 3) · (a² + b² + a·b)

Rektangulära baser (botten L₁×W₁, topp L₂×W₂):
A_botten = L₁·W₁, A_top = L₂·W₂ ⇒ V = (h / 3) · (L₁W₁ + L₂W₂ + √(L₁W₁·L₂W₂))

Sanity checks. Om toppen är lika med botten (A_top = A_botten), blir formen ett prisma och V = A_botten·h. Om toppen är 0, är det en full pyramid och V = (A_botten·h)/3.

Förberäknade exempel (alla indata i cm; volymer i cm³)

Läge	Bottenmått	Toppmått	h	Volym
Kvadratisk	a × a = 10 × 10	b × b = 6 × 6	12	784
Kvadratisk	a × a = 5 × 5	b × b = 5 × 5	8	200
Kvadratisk	a × a = 20 × 20	b × b = 10 × 10	15	3,500
Kvadratisk	a × a = 7.5 × 7.5	b × b = 3.2 × 3.2	18	542.94
Rektangulär	L₁×W₁ = 12 × 8	L₂×W₂ = 6 × 4	20	1,120
Rektangulär	L₁×W₁ = 50 × 40	L₂×W₂ = 30 × 20	35	43,113.5263
Rektangulär	L₁×W₁ = 15 × 10	L₂×W₂ = 15 × 5	12	1,324.2641

Alla värden dubbelkontrollerade med V = (h/3)(A_botten + A_top + √(A_bottenA_top)). Avrundning visas till 2–4 decimaler där det är användbart.

Praktiska tips & kvalitetskontroller

Håll enheterna konsekventa. Ange alla linjära dimensioner i samma enhet; kalkylatorn konverterar till volym i den enheten³ (t.ex. cm → cm³).
Mät höjd korrekt. Använd det vinkelräta avståndet mellan baserna (inte en sned kant).
Använd Ytor-läge när du redan känner till basytorna (från ritningar, CAD eller platsmått) för att undvika att runda fel.
Sanity check med extremvärden: Om b → a, bör resultatet närma sig A·h. Om b → 0, bör resultatet närma sig (A·h)/3.
Precision kontroll: Öka “Decimaler” när indata är små eller när du planerar att kedja beräkningar (t.ex. till massa med hjälp av densitet).

CalcuLife.com