Ten kalkulator online oblicza objętość ściętego stożka (frustum) dla podstaw kwadratowych i prostokątnych. Wykorzystuje standardowy wzór na objętość frustum z zachowaniem spójności jednostek i kontroli precyzji. Metoda opiera się na klasycznej geometrii (zobacz Frustum – Objętość), więc wyniki są matematycznie wiarygodne, gdy dane wejściowe są poprawne (wymiary nieujemne z górną/bazową w tej samej jednostce). Narzędzie to jest szczególnie przydatne dla użytkowników w Polsce, którzy często muszą obliczać objętości w kontekście budownictwa i projektowania.

Kalkulator objętości stożka ściętego
Objętość
—
—
h L W
Podsumowanie danych wejściowych
Wzór
V = (h / 3) · (Abottom + Atop + √(Abottom · Atop))
Kwadratowy: Abottom=a², Atop=b² ⇒ V = (h/3)(a² + b² + ab)
Prostokątny: Abottom=L₁·W₁, Atop=L₂·W₂
Wizualizacja używa stałej projekcji aksonometrycznej: górne i dolne prostokąty pozostają równoległe i wyśrodkowane; pionowe krawędzie skalują się z Twoją wysokością. Wskazówki oznaczają L (niebieski), W (zielony) i h (czerwony).
Udostępnić to?
WhatsApp X Telegram Facebook LinkedIn Reddit

Jak korzystać

  1. Wybierz tryb Kwadratowy, Prostokątny lub Powierzchnie.
  2. Wprowadź:
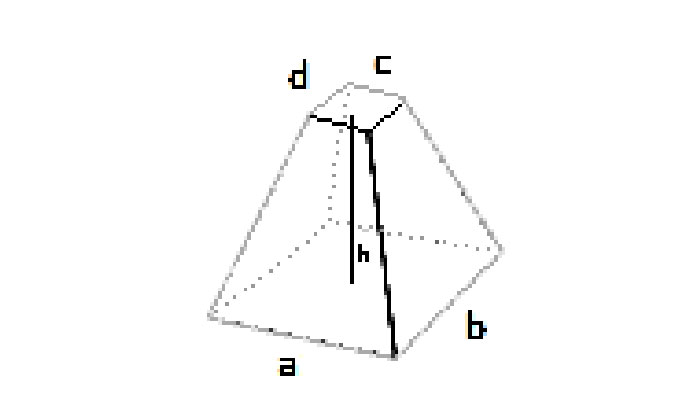
    • Kwadratowy: dolny bok a, górny bok b, wysokość h.
    • Prostokątny: dolny L₁ × W₁, górny L₂ × W₂, wysokość h.
    • Powierzchnie: dolna powierzchnia Abottom, górna powierzchnia Atop, wysokość h.
  3. Wybierz jednostkę i precyzję dziesiętną, a następnie kliknij Oblicz.
  4. Wizualizacja odzwierciedla Twoje proporcje: niebieski ≈ długość (L), zielony ≈ szerokość (W), czerwony ≈ wysokość (h). Pigułka poniżej pokazuje Twoje dane wejściowe do skopiowania/wklejenia.

Wzory

Ogólna objętość frustum

V = (h / 3) · (Abottom + Atop + √(Abottom · Atop))

Podstawy kwadratowe (dolny bok a, górny bok b):
Abottom = a², Atop = b² ⇒ V = (h / 3) · (a² + b² + a·b)

Podstawy prostokątne (dolny L₁×W₁, górny L₂×W₂):
Abottom = L₁·W₁, Atop = L₂·W₂ ⇒ V = (h / 3) · (L₁W₁ + L₂W₂ + √(L₁W₁·L₂W₂))

Kontrole sanity. Jeśli górna równa się dolnej (Atop = Abottom), kształt staje się pryzmatem i V = Abottom·h. Jeśli górna wynosi 0, to jest to pełny stożek i V = (Abottom·h)/3.

Kalkulator objętości stożka ściętego

Przykłady wstępnie obliczone (wszystkie dane w cm; objętości w cm³)

TrybWymiary dolneWymiary górnehObjętość
Kwadratowya × a = 10 × 10b × b = 6 × 612784
Kwadratowya × a = 5 × 5b × b = 5 × 58200
Kwadratowya × a = 20 × 20b × b = 10 × 10153,500
Kwadratowya × a = 7.5 × 7.5b × b = 3.2 × 3.218542.94
ProstokątnyL₁×W₁ = 12 × 8L₂×W₂ = 6 × 4201,120
ProstokątnyL₁×W₁ = 50 × 40L₂×W₂ = 30 × 203543,113.5263
ProstokątnyL₁×W₁ = 15 × 10L₂×W₂ = 15 × 5121,324.2641

Wszystkie wartości poddane podwójnej weryfikacji z V = (h/3)(Abottom + Atop + √(AbottomAtop)). Zaokrąglenie pokazane do 2–4 miejsc dziesiętnych, gdzie to pomocne.

Praktyczne wskazówki i kontrole jakości

  • Utrzymuj spójność jednostek. Wprowadź wszystkie wymiary liniowe w tej samej jednostce; kalkulator przelicza na objętość w tej jednostce³ (np. cm → cm³).
  • Dokładnie zmierz wysokość. Użyj prostopadłej odległości między podstawami (nie krawędzi skośnej).
  • Użyj trybu Powierzchnie, gdy już znasz powierzchnie podstaw (z rysunków, CAD lub pomiarów na miejscu), aby uniknąć kumulacji błędu zaokrąglenia.
  • Kontrola sanity z ekstremami: Jeśli b → a, wynik powinien zbliżać się do A·h. Jeśli b → 0, wynik powinien zbliżać się do (A·h)/3.
  • Kontrola precyzji: Zwiększ „Miejsca dziesiętne”, gdy dane wejściowe są małe lub gdy planujesz łączyć obliczenia (np. do masy przy użyciu gęstości).

CalcuLife.com