台形面積計算機は、標準的な幾何学の公式を使用して、台形の2つの底辺と高さから面積を求めます。必要な入力は、上底 a、下底 b、および垂直の高さ h の長さだけです。視覚化は、あなたの数値に合わせて中心に配置され、どの辺がどれかを確認できます。この計算機は、日本の学生や専門家にとって、幾何学の学習や実務に役立つツールです。
台形面積計算機
計算機の仕組み
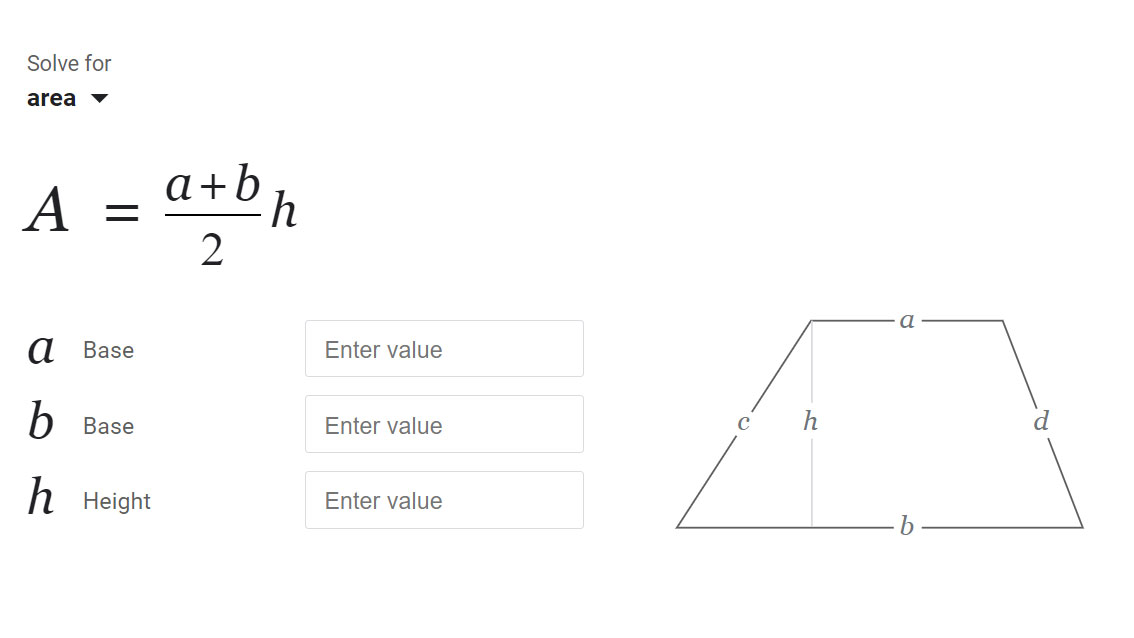
- 入力: 上底 a、下底 b、高さ h(すべて正の実数)。
- 公式:
面積 = ((a + b) / 2) × h。公式の簡潔な参照については、Wolfram MathWorld: Trapezoidを参照してください。 - 単位: 出力は平方単位です。入力がメートルの場合、結果はm²; インチの場合はin²です。このツールは、どの文脈にも適合するように単位を一般的に保ちます。
- 視覚化: 図は常にキャンバスの中心に留まり、入力した同じ量をラベル付けします: 上に a、下に b、そしてそれらの間の垂直距離を h とします。
- 数値の安定性: ツールは小数、大きな値、小さな値を受け入れます。内部の精度を保ちながら、表示をきれいに丸めます。
この公式が正しい理由
台形の面積は、高さと2つの平行な辺の平均の積に等しいです。直感的には、短い底辺を高さに沿って「スライド」させると、台形を2つの底辺の平均が幅となる長方形に再配置できます。これにより、A = h × (a + b)/2が得られます。
ステップバイステップの例
- 例 1(デフォルトの図に一致):
- a = 6, b = 10, h = 4
- 底辺の平均 = (6 + 10)/2 = 8
- 面積 = 8 × 4 = 32 平方単位
- 例 2(小数):
- a = 3.5, b = 12, h = 2.8
- 底辺の平均 = (3.5 + 12)/2 = 7.75
- 面積 = 7.75 × 2.8 = 21.7 平方単位
- 例 3(細い高さ):
- a = 20, b = 24, h = 0.5
- 底辺の平均 = 22
- 面積 = 22 × 0.5 = 11 平方単位
必要な逆計算
- 面積と底辺から高さを求める:
h = (2 × 面積) / (a + b) - 面積、他の底辺、高さから未知の底辺を求める:
a = (2 × 面積) / h − b(または a と b を入れ替えます)
高さとは何か
高さは底辺に垂直です。 斜めの側面ではありません。側面が傾いている場合でも、高さは2つの底辺の間の最短の直線距離です。直角または二等辺台形ではこれが簡単に見えますが、鈍角の場合でも垂直のままです。
品質チェックとエッジケース
- 正の値: すべての入力は面積を生成するためにゼロより大きくなければなりません。
- 底辺が等しい: a = b の場合、台形は長方形になり、公式は
A = b × hに簡略化されます。 - 非常に大きな数または非常に小さな数: 面積は高さと底辺の平均に対して線形にスケールします。すべての入力を2倍にすると、高さに対して面積も2倍になり、底辺の平均に対しても適切に2倍になります。
現実世界の台形の形状
- 道路の断面と中央分離帯: 側面から見ると、肩や土手はしばしば台形を形成します。
- 屋根のフレーミング: 一部の寄棟屋根や小屋根パネル、ファシアプロファイルは台形です。
- 造園用ベッドとスロープ: 平面図や側面プロファイルは頻繁に台形を生じます。
- 板金部品とタイル: 台形のブランクは製造や床レイアウトで一般的です。
- 溝やチャネル: 工学的な溝の断面はしばしば台形のプロファイルを使用します。
結果の利用
- 材料の見積もり: 面積に厚さを掛けて体積を近似します(例: 土壌やコンクリート)。単位の一貫性を保ちます。
- コスト計算: 材料が平方単位あたりの価格である場合、単位コストに面積を掛けて支出を見積もります。
- 図面のスケーリング: 入力がスケールされた計画から来た場合、面積を計算する前に実世界の単位に変換します。
避けるべき一般的な間違い
- 垂直の高さの代わりに斜めの側面を使用すること。
- 単位を不正に追加すること。すべての入力を同じ単位に保ち、出力がその単位の平方になるようにします。
- 公式が底辺の平均を使用することを忘れること、差ではありません。
CalcuLife.com





コメントする