Este calculador en línea calcula el volumen de una pirámide truncada (frustum) tanto para bases cuadradas como rectangulares. Implementa la fórmula estándar del volumen del frustum con un manejo de unidades consistente y control de precisión. El método se basa en la geometría clásica (ver Frustum – Volumen), por lo que los resultados son matemáticamente fiables cuando las entradas son válidas (dimensiones no negativas con la parte superior/base en la misma unidad). Este tipo de herramienta es especialmente útil en países de habla hispana donde la construcción y la arquitectura requieren cálculos precisos.
Cuadrado: Ainferior=a², Asuperior=b² ⇒ V = (h/3)(a² + b² + ab)
Rectangular: Ainferior=L₁·W₁, Asuperior=L₂·W₂
Cómo Usar
- Elige el modo Cuadrado, Rectangular o Áreas.
- Ingresa:
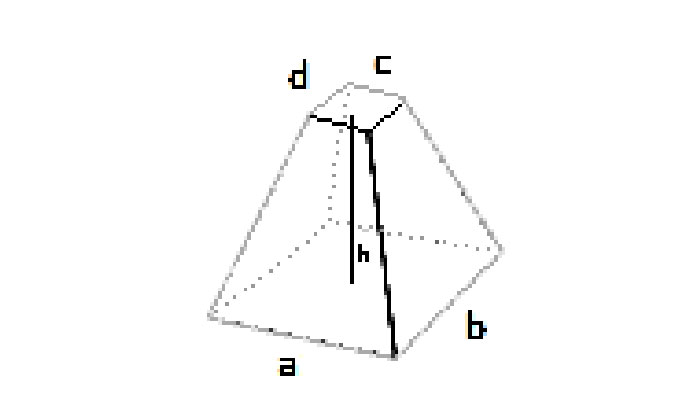
- Cuadrado: lado inferior a, lado superior b, altura h.
- Rectangular: base L₁ × W₁, parte superior L₂ × W₂, altura h.
- Áreas: área inferior Abottom, área superior Atop, altura h.
- Selecciona la unidad y la precisión decimal, luego haz clic en Calcular.
- La visualización refleja tus proporciones: azul ≈ longitud (L), verde ≈ ancho (W), rojo ≈ altura (h). La pastilla de abajo muestra tus entradas para copiar/pegar.
Fórmulas
Volumen general del frustum
V = (h / 3) · (Abottom + Atop + √(Abottom · Atop))
Bases cuadradas (lado inferior a, lado superior b):
Abottom = a², Atop = b² ⇒ V = (h / 3) · (a² + b² + a·b)
Bases rectangulares (base L₁×W₁, parte superior L₂×W₂):
Abottom = L₁·W₁, Atop = L₂·W₂ ⇒ V = (h / 3) · (L₁W₁ + L₂W₂ + √(L₁W₁·L₂W₂))
Comprobaciones de sensatez. Si la parte superior es igual a la inferior (Atop = Abottom), la forma se convierte en un prisma y V = Abottom·h. Si la parte superior es 0, es una pirámide completa y V = (Abottom·h)/3.
Ejemplos Pre-calculados (todas las entradas en cm; volúmenes en cm³)
| Modo | Dimensiones inferiores | Dimensiones superiores | h | Volumen |
|---|---|---|---|---|
| Cuadrado | a × a = 10 × 10 | b × b = 6 × 6 | 12 | 784 |
| Cuadrado | a × a = 5 × 5 | b × b = 5 × 5 | 8 | 200 |
| Cuadrado | a × a = 20 × 20 | b × b = 10 × 10 | 15 | 3,500 |
| Cuadrado | a × a = 7.5 × 7.5 | b × b = 3.2 × 3.2 | 18 | 542.94 |
| Rectangular | L₁×W₁ = 12 × 8 | L₂×W₂ = 6 × 4 | 20 | 1,120 |
| Rectangular | L₁×W₁ = 50 × 40 | L₂×W₂ = 30 × 20 | 35 | 43,113.5263 |
| Rectangular | L₁×W₁ = 15 × 10 | L₂×W₂ = 15 × 5 | 12 | 1,324.2641 |
Todos los valores verificados dos veces con V = (h/3)(Abottom + Atop + √(AbottomAtop)). Redondeo mostrado a 2–4 decimales donde sea útil.
Consejos Prácticos & Comprobaciones de Calidad
- Mantén las unidades consistentes. Ingresa todas las dimensiones lineales en la misma unidad; el calculador convierte a volumen en esa unidad³ (por ejemplo, cm → cm³).
- Mide la altura correctamente. Usa la distancia perpendicular entre las bases (no un borde inclinado).
- Usa el modo Áreas cuando ya conozcas las áreas de las bases (de dibujos, CAD o mediciones en el sitio) para evitar errores de redondeo acumulativos.
- Comprobación de sensatez con extremos: Si b → a, el resultado debería acercarse a A·h. Si b → 0, el resultado debería acercarse a (A·h)/3.
- Control de precisión: Aumenta “Decimales” cuando las entradas son pequeñas o cuando planeas encadenar cálculos (por ejemplo, a masa usando densidad).
CalcuLife.com






Ha sido una excelente ayuda, superando una IA ofrecida por Bing.com, que me mereció dudas en el resultado. Sin embargo y en honor a la verdad debo decir que vuestro sitio también lo encontré en ese mismo buscador.
Muchísimas gracias!.
Muchas gracias!