사다리꼴 면적 계산기는 표준 기하학 공식을 사용하여 두 개의 밑변과 높이로부터 사다리꼴의 면적을 찾습니다. 필요한 입력값은 위쪽 밑변 a, 아래쪽 밑변 b, 그리고 수직 높이 h의 길이입니다. 시각화는 입력한 숫자에 맞춰 중앙에 위치하고 크기를 조정하여 각 변이 무엇인지 확인할 수 있습니다. 이 도구는 한국의 다양한 건축 및 디자인 프로젝트에서 유용하게 사용될 수 있습니다.

사다리꼴 면적 계산기
h=0 a=0 b=0
이걸 공유하시겠어요?
WhatsApp X Telegram Facebook LinkedIn Reddit

계산기 작동 방식

  • 입력값: 위쪽 밑변 a, 아래쪽 밑변 b, 높이 h (모두 양의 실수).
  • 공식: 면적 = ((a + b) / 2) × h. 공식에 대한 간단한 참조는 Wolfram MathWorld: Trapezoid를 참조하세요.
  • 단위: 출력은 제곱 단위로 표시됩니다. 입력값이 미터일 경우 결과는 m²로, 인치일 경우 in²로 표시됩니다. 이 도구는 모든 맥락에 맞게 단위를 일반적으로 유지합니다.
  • 시각화: 다이어그램은 항상 캔버스 중앙에 위치하며 입력한 동일한 양을 레이블로 표시합니다: 위쪽에 a, 아래쪽에 b, 그리고 두 밑변 사이의 수직 거리 h로 표시됩니다.
  • 수치 안정성: 이 도구는 소수, 큰 값 및 작은 값을 모두 수용합니다. 내부 정밀도를 유지하면서 표시를 깔끔하게 반올림합니다.

이 공식이 올바른 이유

사다리꼴의 면적은 높이에 두 개의 평행한 변의 평균을 곱한 값과 같습니다. 직관적으로, 짧은 밑변을 높이에 따라 “슬라이드”하면 사다리꼴을 두 밑변의 평균 너비를 가진 직사각형으로 재배치할 수 있습니다. 이는 A = h × (a + b)/2를 제공합니다.

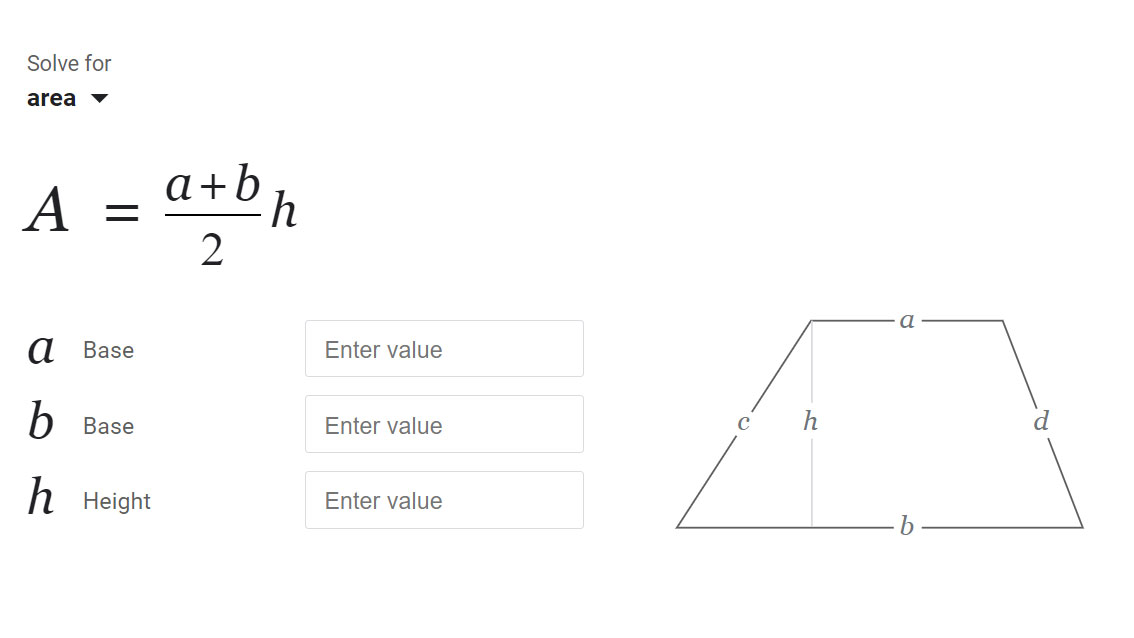
시각화가 포함된 사다리꼴 면적 계산기

단계별 예시

  1. 예시 1 (기본 도면과 일치):
    • a = 6, b = 10, h = 4
    • 밑변의 평균 = (6 + 10)/2 = 8
    • 면적 = 8 × 4 = 32 제곱 단위
  2. 예시 2 (소수):
    • a = 3.5, b = 12, h = 2.8
    • 밑변의 평균 = (3.5 + 12)/2 = 7.75
    • 면적 = 7.75 × 2.8 = 21.7 제곱 단위
  3. 예시 3 (얇은 높이):
    • a = 20, b = 24, h = 0.5
    • 밑변의 평균 = 22
    • 면적 = 22 × 0.5 = 11 제곱 단위

필요할 수 있는 역산

  • 면적과 밑변이 주어졌을 때 높이 구하기:
    h = (2 × 면적) / (a + b)
  • 면적, 다른 밑변 및 높이가 주어졌을 때 미지의 밑변 구하기:
    a = (2 × 면적) / h − b (또는 a와 b를 바꿉니다)

높이의 정의

높이는 밑변에 수직입니다. 경사진 변이 아닙니다. 변이 기울어져 있더라도 높이는 여전히 두 밑변 사이의 가장 짧은 직선 거리입니다. 직각 또는 이등변 사다리꼴에서는 쉽게 확인할 수 있으며, 둔각의 경우에도 여전히 수직입니다.

품질 검사 및 경계 사례

  • 양수 조건: 면적을 생성하기 위해서는 세 입력값 모두 0보다 커야 합니다.
  • 같은 밑변: a = b일 경우, 사다리꼴은 직사각형이 되며; 공식은 A = b × h로 단순화됩니다.
  • 매우 큰 수 또는 매우 작은 수: 면적은 높이와 밑변의 평균에 따라 선형적으로 변합니다. 모든 입력값을 두 배로 하면 높이에 대한 면적이 두 배가 되고, 밑변의 평균에 대해서도 적절히 두 배가 됩니다.

실제 사다리꼴 형태

  • 도로 단면 및 중앙 분리대: 어깨와 둔덕은 측면에서 볼 때 종종 사다리꼴을 형성합니다.
  • 지붕 구조: 일부 힙 또는 창고 지붕 패널과 처마 프로파일은 사다리꼴입니다.
  • 조경 침대 및 경사로: 평면도와 측면 프로파일은 자주 사다리꼴을 생성합니다.
  • 판금 부품 및 타일: 사다리꼴 블랭크는 제조 및 바닥 배치에서 일반적입니다.
  • 도랑 및 채널: 공학적 단면의 도랑은 종종 사다리꼴 프로파일을 사용합니다.

결과 사용하기

  • 재료 추정: 면적에 두께를 곱하여 부피를 대략적으로 추정합니다 (예: 흙 또는 콘크리트). 단위 일관성을 유지하세요.
  • 비용 산정: 재료가 제곱 단위당 가격이 매겨진 경우, 단가에 면적을 곱하여 지출을 추정합니다.
  • 도면 스케일링: 입력값이 스케일된 계획에서 온 경우, 면적을 계산하기 전에 실제 단위로 변환하세요.

피해야 할 일반적인 실수

  • 수직 높이 대신 경사진 변을 사용하는 것.
  • 단위를 잘못 추가하는 것. 모든 입력값을 동일한 단위로 유지하여 출력이 해당 단위의 제곱으로 나오도록 합니다.
  • 공식이 밑변의 평균을 사용한다는 것을 잊는 것, 그들의 차이가 아닙니다.

CalcuLife.com